Musisz udowodnić, że trójkąt, którego wierzchołkami są środki boków trójkąta równoramiennego, też jest równoramienny.
Naszkicujmy rysunek poglądowy. Trójkąt równoramienny ABC, a środki boków tego trójkąta oznaczmy jako DEF. Tworzą one mniejszy trójkąt. Oznaczmy odcinki AE i EB jako a. Odcinki AD, DC, CF oraz FB oznaczmy jako b.
Twierdzenie: Linia środkowa jest równoległa do odpowiadającego jej boku. Jej długość jest dwukrotnie mniejsza od długości tego boku. Linia środkowa trójkąta to linia łącząca środki boków trójkąta – zatem są to odcinki DF, DE oraz EF .
Zatem linia środkowa DF jest równoległa do AB, czyli jej długość:
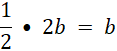
Analogicznie linia środkowa EF jest równoległa do boku AC, zatem ma długość:
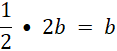
Tak samo DE jest równoległa do BC, zatem jej długość: 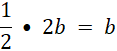
Widzimy, że trójkąt, który powstał ma boki o długości b, b i a – jest równoramienny, co należało udowodnić

Uzasadniono podaną tezę.

Zadanie 1
75Zadanie 2
75Zadanie 5
76Zadanie 6
76Zadanie 8
76Zadanie 10
77Zadanie 11
77Zadanie 12
77Zadanie 15
78Zadanie 19
78Ćwiczenie B
79Zadanie 1
83Zadanie 2
83Zadanie 3
83Zadanie 5
84Zadanie 7
84Zadanie 8
84Zadanie 9
85Zadanie 15
85Zadanie 1
88Zadanie 2
88Zadanie 9
89Zadanie 13
90Zadanie 22
91Zadanie 23
91Zadanie 25
92Ćwiczenie A
93Zadanie 1
95Zadanie 2
95Zadanie 5
95Zadanie 6
95Zadanie 7
95Zadanie 1
99Zadanie 2
99Zadanie 3
99Zadanie 4
99Zadanie 6
100Zadanie 9
100Zadanie 10
100Ćwiczenie C
102Ćwiczenie E
103Zadanie 1
104Zadanie 3
104Zadanie 8
105Zadanie 9
105Zadanie 10
105Zadanie 11
105Zadanie 6
109Zadanie 7
109Zadanie 11
110Zadanie 5
112Zadanie 7
113Zadanie 2
114Zadanie 4
114Zadanie 12
115Zadanie 22
115Zadanie 29
116Zadanie 33
116Zadanie 35
117Zadanie 36
117
