Zbiór zadań, Wydawnictwo: Nowa Era

Zadanie 19 - strona 244

W tym zadaniu musisz wyznaczyć wszystkie możliwe wzory na funkcje kwadratowe o współczynnikach ze zbioru $\text{[math]}$ i wyznaczyć ich wierzchołki.

1 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

2 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

3 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

4 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

5 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

6 możliwość:

$\text{[math]}$

$\text{[math]}$

Współrzędne wierzchołka:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Wyznaczmy z twierdzenia Pitagorasa odległości wierzchołków od punktu $\text{[math]}$ :

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Najmniejszą odległość ma wierzchołek numer 4 albo numer 5. Sprowadźmy je do wspólnego mianownika i porównajmy:

$\text{[math]}$

$\text{[math]}$

Mniejsza odległość jest dla funkcji szóstej, czyli $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

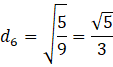
Wyznacz wszystkie możliwości (jest ich 6) i wyznacz współrzędne wierzchołków każdej funkcji. Pierwszą współrzędną możesz obliczyć ze wzoru $\text{[math]}$ , a drugą wyliczając wartość funkcji dla argumentu $\text{[math]}$ . Odległości punktów od punktu $\text{[math]}$ możesz wyliczyć z twierdzenia Pitagorasa.

Zadanie 15.1., strona 318, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie Co było na lekcji 1., strona 32, Matematyka. Klasa 6. Zeszyt ćwiczeń. Część 2 - rozwiązania i odpowiedzi

Zadanie 10, strona 138, Matematyka z kluczem. Klasa 5. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Ćwiczenie 10, strona 288, Matematyka wokół nas. Klasa 4. Podręcznik - rozwiązania i odpowiedzi

Zadanie 4, strona 9, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Zadanie 14., strona 70, Matematyka. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie 3., strona 43, Matematyka z plusem. Arytmetyka. Klasa 4. Zeszyt ćwiczeń. Wersja B. Część 1 – rozwiązania i odpowiedzi

Ćwiczenie 11, strona 98, Matematyka z plusem. Klasa 5. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 1., strona 193, To się liczy! Klasa 1. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1., strona 75, Matematyka. Klasa 4. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

236

Zadanie 2

236

236

236

236

Zadanie 4

236

236

236

236

236

236

236

236

236

236

236

236

Zadanie 10

236

236

236

236

236

Zadanie 11

237

237

237

237

237

Zadanie 12

237

237

237

237

Zadanie 13

237

237

237

237

Zadanie 14

237

237

237

237

237

238

238

238

238

238

Zadanie 21

238

238

238

238

238

238

238

238

238

Zadanie 1

239

239

239

239

239

239

239

Zadanie 2

239

239

239

239

239

Zadanie 3

239

239

239

239

239

Zadanie 4

239

239

239

239

239

239

239

240

240

240

Zadanie 12

240

240

240

240

240

240

240

240

240

240

Zadanie 18

240

240

240

240

240

240

240

241

241

Zadanie 21

241

241

241

241

241

Zadanie 24

241

241

241

241

Zadanie 25

241

241

241

Zadanie 26

241

241

241

241

Zadanie 1

242

242

242

242

242

242

242

Zadanie 2

242

242

242

242

242

Zadanie 3

242

242

242

242

242

242

242

Zadanie 4

242

242

242

242

242

242

242

Zadanie 5

242

242

242

242

242

242

242

243

243

Zadanie 8

243

243

243

243

243

243

243

Zadanie 9

243

243

243

243

243

243

243

Zadanie 12

243

243

243

243

Zadanie 14

244

244

244

244

244

244

244

244

244

244

244

Zadanie 21

244

244

244

244

244

244

Zadanie 1

245

245

245

245

245

Zadanie 2

245

245

245

245

245

Zadanie 3

245

245

245

245

245

245

245

Zadanie 4

245

245

245

245

Zadanie 5

245

245

245

245

Zadanie 6

245

245

245

245

245

245

245

246

246

Zadanie 11

246

246

246

246

246

Zadanie 13

246

246

246

246

Zadanie 14

246

246

246

Zadanie 15

246

246

246

Zadanie 16

246

246

246

246

246

246

Zadanie 19

246

246

246

Zadanie 20

247

247

247

Zadanie 21

247

247

247

Zadanie 22

247

247

247

247

247

Zadanie 23

247

247

247

247

247

247

247

247

247

Zadanie 29

247

247

247

247

248

248

Zadanie 3

248

248

248

248

248

248

Zadanie 7

248

248

248

248

248

Zadanie 8

248

248

248

248

248

Zadanie 9

248

248

248

248

248

248

Zadanie 11

249

249

249

249

249

Zadanie 14

249

249

249

249

249

249

249

Zadanie 19

249

249

249

Zadanie 20

250

250

250

250

250

250

250

250

250

Zadanie 25

250

250

250

Zadanie 26

250

250

250

Zadanie 27

250

250

250

250

250

Zadanie 29

251

251

251

251

251

Zadanie 32

251

251

251

251

251

Zadanie 34

251

251

251

252

252

252

252

252

252

252

252

252

253

253

253

253

253

253

Pełny spis treści