Prosta AB:
![]()
Wysokość wychodząca z wierzchołka C:
![]()
Prosta BC:
![]()
![]()
![]()
![]()
![]()
Wysokość wychodząca z wierzchołka A:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ortocentrum:
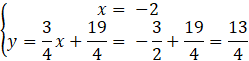
![]()

By wyznaczyć współrzędne punktu przecięcia wysokości, wyznacz najpierw wzory prostych, które te wysokości zawierają.
Wysokość wychodząca z wierzchołka C musi być prostopadła do boku AB, który zawiera się w prostej y = 1, a także przechodzić przez punkt C. Stąd wiesz, że należy ona do prostej x = -2.
Wysokość wychodząca z wierzchołka musi być prostopadła do prostej zawierającej bok BC, a więc iloczyn współczynników kierunkowych tych prostych musi być równy -1. Współczynnik kierunkowy prostej BC oblicz z układu równań, który powstaje przez postawienie współrzędnych punktów B i C do równania prostej. Wysokość musi również przechodzić przez punkt A, na tej postawie utwórz równanie, które pozwala wyznaczyć wartość współczynnika B.
Aby obliczyć punkt przecięcia wysokości utwórz układ równań, składający się z dwóch równań prostych zawierających wysokości.