Wiedząc, że doświadczenie polega wyciągnięciu kuli, ze zwracaniem, z jednego z trzech pudeł typu I lub jednego z dwóch pudeł typu II, gdzie odpowiednio znajdują się 2 kule białe i 4 czarne oraz 3 kule białe i 3 czarne, określ szansę na trzykrotne wyciągnięcie kuli czarnej, przy 5 powtórzeniach tego doświadczenia.
Prawdopodobieństwo wybrania pudełka typu I wynosi
![]() , a typu II -
, a typu II -
![]() .
.
Prawdopodobieństwo wylosowania białej kuli z pudełka typu I wynosi
![]() , a czarnej -
, a czarnej -
![]() .
.
Prawdopodobieństwo wylosowania białej kuli z pudełka typu II wynosi
![]() , a czarnej -
, a czarnej -
![]() .
.
Narysuj drzewko:
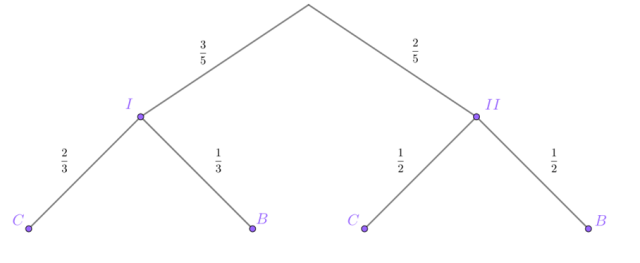
A – zdarzenie, w którym przy 5 próbach, wylosowano trzy czarne kule.
B – zdarzenie, w którym wylosowano czarną kulę.
Oblicz prawdopodobieństwo wylosowania kuli czarnej:
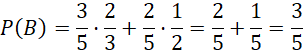
Wykorzystaj schemat Bernoulliego do obliczenia P(A):
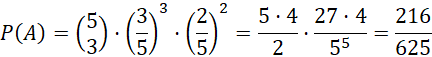

Na początku określ prawdopodobieństwo wylosowania jednego z typów pudełka, oraz poszczególne szanse na wylosowanie kuli danego koloru z danego typu pudełka. Następnie narysuj drzewko z odpowiednimi danymi. Wykorzystaj drzewko i oblicz szansę na wylosowanie czarnej kuli. Potem skorzystaj ze schematu Bernoulliego
![]() , gdzie p to prawdopodobieństwo pewnego zdarzenia, q to zdarzenie przeciwne do q, n to ilość wykonanych testów, a k to oczekiwana ilość wystąpień i oblicz P(A).
, gdzie p to prawdopodobieństwo pewnego zdarzenia, q to zdarzenie przeciwne do q, n to ilość wykonanych testów, a k to oczekiwana ilość wystąpień i oblicz P(A).

Zadanie 4.1.
70Zadanie 4.2.
70Zadanie 4.3.
70Zadanie 4.4.
70Zadanie 4.5.
70Zadanie 4.6.
71Zadanie 4.7.
71Zadanie 4.8.
71Zadanie 4.9.
71Zadanie 4.10.
71Zadanie 4.11.
71Zadanie 4.12.
72Zadanie 4.13.
72Zadanie 4.14.
72Zadanie 4.15.
72Zadanie 4.16.
72Zadanie 4.17.
73Zadanie 4.18.
73Zadanie 4.19.
73Zadanie 4.20.
73Zadanie 4.25.
74Zadanie 4.28.
74Zadanie 4.29.
74Zadanie 4.30.
74Zadanie 4.36.
75Zadanie 4.38.
75Zadanie 4.39.
75Zadanie 4.40.
76Zadanie 4.41.
76Zadanie 4.45.
76Zadanie 4.46.
76Zadanie 4.47.
77Zadanie 4.50.
77Zadanie 4.51.
77Zadanie 4.53.
78Zadanie 4.54.
78Zadanie 4.55.
78Zadanie 4.56.
79Zadanie 4.57.
79Zadanie 4.58.
79Zadanie 4.59.
79Zadanie 4.60.
79Zadanie 4.61.
80Zadanie 4.62.
80Zadanie 4.63.
80Zadanie 4.64.
80Zadanie 4.65.
80Zadanie 4.66.
81Zadanie 4.67.
81Zadanie 4.68.
81Zadanie 4.70.
81Zadanie 4.74.
81Zadanie 4.81.
82Zadanie 4.82.
83Zadanie 4.83.
83Zadanie 4.84.
83Zadanie 4.85.
83Zadanie 4.86.
83Zadanie 4.87.
83Zadanie 4.88.
83Zadanie 4.89.
84Zadanie 4.93.
84Zadanie 4.94.
84Zadanie 4.95.
84Zadanie 4.96.
84Zadanie 4.97.
85Zadanie 4.98.
85Zadanie 4.99.
85Zadanie 4.100.
85Zadanie 4.101.
85Zadanie 4.102.
85Zadanie 4.103.
86Zadanie 4.104.
86Zadanie 4.106.
86Zadanie 4.107.
86Zadanie 4.109.
86Zadanie 4.111.
87Zadanie 4.116.
87Zadanie 4.118.
88Zadanie 4.119.
88Zadanie 4.120.
88Zadanie 4.121.
88Zadanie 4.128.
89Zadanie 4.129.
89Zadanie 4.130.
89Zadanie 4.131.
89Zadanie 4.132.
90Zadanie 4.133.
90Zadanie 4.134.
90Zadanie 4.135.
90Zadanie 4.136.
90Zadanie 4.137.
91Zadanie 4.138.
91Zadanie 4.139.
91Zadanie 4.140.
91Zadanie 4.141.
91Zadanie 4.145.
92Zadanie 4.146.
92Zadanie 4.147.
92Zadanie 4.148.
92Zadanie 4.149.
93Zadanie 4.150.
93Zadanie 4.153.
94Zadanie 4.154.
94Zadanie 4.157.
94Zadanie 4.162.
95Zadanie 4.172.
97Zadanie 4.173.
97Zadanie 4.174.
97Zadanie 4.179.
98Zadanie 4.185.
99Zadanie 4.219.
104Zadanie 4.188.
99Zadanie 4.189.
99Zadanie 4.190.
100Zadanie 4.193.
100Zadanie 4.194.
100Zadanie 4.195.
100Zadanie 4.197.
101Zadanie 4.198.
101Zadanie 4.199.
101Zadanie 4.200.
101Zadanie 4.201.
101Zadanie 4.202.
101Zadanie 4.203.
101Zadanie 4.211.
102Zadanie 4.212.
103Zadanie 11.
106Zadanie 12.
106Zadanie 13.
107Zadanie 15.
107Zadanie 17.
107Zadanie 18.
107Zadanie 19.
107Zadanie 20.
108Zadanie 22.
108Zadanie 23.
108Zadanie 24.
108Zadanie 25.
108Zadanie 26.
109Zadanie 27.
109Zadanie 28.
109Zadanie 31.
109Zadanie 32.
109Zadanie 38.
110Zadanie 39.
110Zadanie 40.
110
