Wyznacz cosinusy kątów, które z podstawą tego ostrosłupa tworzą jego krawędzie boczne, jeśli jego podstawą jest trójkąt o bokach 6, 8 i 10, a wszystkie krawędzie boczne mają długość 13.
Trójkąt o bokach 6, 8, 10 jest prostokątny.
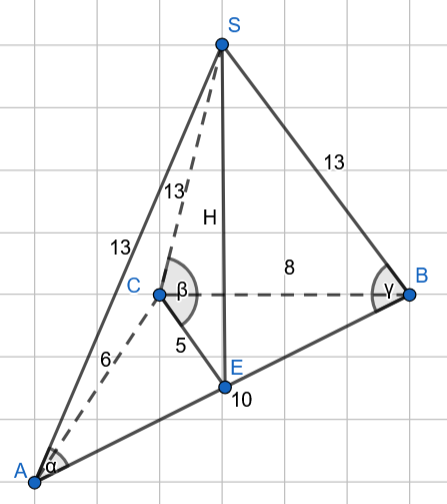
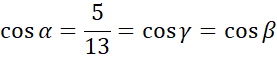

Zauważ, że ostrosłup jest prosty, ponieważ wszystkie jego krawędzie boczne mają taką samą długość, więc wysokość opada na środek okręgu opisanego na jego podstawie - środek przeciwprostokątnej. Więc odcinki AE, BE i CE będą promieniem okręgu opisanego na podstawie.
Skorzystaj z twierdzenia Pitagorasa i wyznacz cosinus podanego kąta.

Ćwiczenie 1
86Ćwiczenie 5
87Zadanie 1
89Zadanie 2
89Zadanie 4
90Zadanie 5
90Ćwiczenie 2
91Ćwiczenie 3
91Ćwiczenie 4
92Ćwiczenie 6
92Zadanie 1
93Zadanie 2
93Zadanie 4
93Zadanie 5
93Ćwiczenie 2
94Ćwiczenie 4
95Ćwiczenie 5
95Zadanie 1
95Zadanie 3
95Zadanie 9
96Ćwiczenie 4
98Ćwiczenie 5
98Zadanie 1
98Zadanie 2
98Ćwiczenie 2
101Ćwiczenie 6
102Ćwiczenie 2
105Ćwiczenie 5
106Ćwiczenie 6
106Ćwiczenie 7
107Zadanie 1
107Zadanie 9
108Ćwiczenie 1
109Zadanie 1
110Zadanie 3
110Zadanie 4
110Ćwiczenie 5
113Ćwiczenie 6
113Zadanie 2
114Zadanie 4
114Zadanie 6
114Ćwiczenie 1
115Ćwiczenie 2
115Ćwiczenie 3
116Zadanie 3
117Ćwiczenie 1
119Ćwiczenie 2
119Ćwiczenie 3
119Ćwiczenie 4
120Ćwiczenie 7
121Zadanie 2
122Ćwiczenie 1
124Ćwiczenie 2
124Zadanie 1
131Zadanie 3
131
