Należy wykazać powyższą tożsamość.
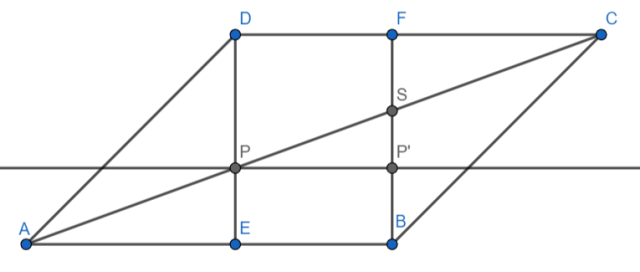
|DE|, |FB| - wskazane w treści wysokości
P, S — punkty przecięcia |AC| kolejno z |DE| i |FB|
![]()
![]()
![]()
Poprowadzimy prostą przechodzącą przez P o prostopadłą do |FB| i przecinają ten odcinek w punkcie P’
![]()
Analogicznie dowodzimy, że |PS| = |SC|.

Niech |DE|, |FB| to wskazane w treści wysokości, zaś P, S to punkty przecięcia |AC| kolejno z |DE| i |FB|. Utworzone trójkąty są równoramienne, czyli ![]()
![]()
![]()
![]()
![]()

Zadanie 4.1.
101Zadanie 4.2.
101Zadanie 4.6.
102Zadanie 4.8.
102Zadanie 4.9.
102Zadanie 4.11.
102Zadanie 4.17.
103Zadanie 4.19.
103Zadanie 4.24.
104Zadanie 4.25.
104Zadanie 4.26.
104Zadanie 4.27.
104Zadanie 4.28.
104Zadanie 4.30.
105Zadanie 4.32.
105Zadanie 4.35.
106Zadanie 4.39.
106Zadanie 4.41.
106Zadanie 4.43.
107Zadanie 4.55.
108Zadanie 4.56.
108Zadanie 4.62.
108Zadanie 4.64.
109Zadanie 4.68.
109Zadanie 4.70.
109Zadanie 4.75.
110Zadanie 4.77.
110Zadanie 4.82.
111Zadanie 4.83.
111Zadanie 4.84.
111Zadanie 4.85.
111Zadanie 4.86.
111Zadanie 4.96.
112Zadanie 4.98.
112Zadanie 4.100.
113Zadanie 4.101.
113Zadanie 4.104.
113Zadanie 4.129.
117Zadanie 4.130.
117Zadanie 4.131.
118Zadanie 4.132.
118Zadanie 4.134
118Zadanie 4.136.
119Zadanie 4.142.
119Zadanie 4.26.
123Zadanie 4.28.
124Zadanie 4.32.
124
