Należy obliczyć długość dłuższej przekątnej trapezu prostokątnego spełniającego warunki zadania.
Z tw. Pitagorasa:
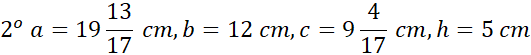
Z tw. Pitagorasa:
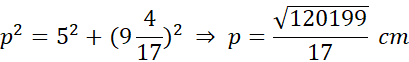
Rozpatrujemy dwa analogiczne przypadki w zależności od długości wysokości i dłuższej podstawy. W obu przypadkach korzystasz z twierdzenia Pitagorasa, ponieważ wysokość wraz z przekątną i dłuższą podstawą pomniejszoną o 
Zadanie 4.1.
101Zadanie 4.2.
101Zadanie 4.6.
102Zadanie 4.8.
102Zadanie 4.9.
102Zadanie 4.11.
102Zadanie 4.17.
103Zadanie 4.19.
103Zadanie 4.24.
104Zadanie 4.25.
104Zadanie 4.26.
104Zadanie 4.27.
104Zadanie 4.28.
104Zadanie 4.30.
105Zadanie 4.32.
105Zadanie 4.35.
106Zadanie 4.39.
106Zadanie 4.41.
106Zadanie 4.43.
107Zadanie 4.55.
108Zadanie 4.56.
108Zadanie 4.62.
108Zadanie 4.64.
109Zadanie 4.68.
109Zadanie 4.70.
109Zadanie 4.75.
110Zadanie 4.77.
110Zadanie 4.82.
111Zadanie 4.83.
111Zadanie 4.84.
111Zadanie 4.85.
111Zadanie 4.86.
111Zadanie 4.96.
112Zadanie 4.98.
112Zadanie 4.100.
113Zadanie 4.101.
113Zadanie 4.104.
113Zadanie 4.129.
117Zadanie 4.130.
117Zadanie 4.131.
118Zadanie 4.132.
118Zadanie 4.134
118Zadanie 4.136.
119Zadanie 4.142.
119Zadanie 4.26.
123Zadanie 4.28.
124Zadanie 4.32.
124