Dane:
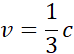
Zacznij od układu. Przyjmij punkt, w którym statek mija Ziemię. Kąt nachylenia osi układu statku ![]()
![]()
![]()
Położenie ciała to:
![]()
gdzie: ![]()
![]()
![]()
![]()
Przy czym:
![]()
![]()
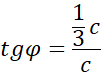
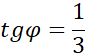
Kąt nachylenia osi ct′ układu związanego ze statkiem do osi x związanej z Ziemią będzie miał postać:
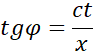
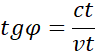
![]()
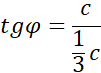
![]()
Osie układu ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Oznacza to, że obie proste, na której leżą osie układu związanego ze statkiem mają zerowy wyraz wolny. Współczynniki kierunkowe tych prostych odpowiadają tangensom kąta nachylenia tych prostych do osi poziomej.
Z tego wynika, że oś czasoprzestrzenna leży na prostej: ![]()
Natomiast oś przestrzenna leży na prostej:
![]()
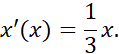
Zaznacz te proste, a na nich osie układu ![]()

Zadanie dotyczy zastosowania transformacji Lorentza do analizy ruchu statku w odniesieniu do Ziemi. Wskazuje się tu na specyfikę relatywistycznych transformacji między różnymi układami odniesienia.
Główny punkt opiera się na interpretacji kątów nachylenia dwóch układów względem siebie. Wykorzystując zależności trygonometryczne oraz definicje prędkości, można znaleźć konkretne wartości dla kątów nachylenia osi tych układów.
Przyjęto, że statek i Ziemia mijają się w pewnym wspólnym punkcie, co jest punktem wyjścia dla analizy. Dzięki znajomości wzorów liniowych i odpowiednich współczynników kierunkowych można przedstawić osie obu układów jako funkcje liniowe, które ilustrują ich względne położenie w przestrzeni.
Podsumowując, zadanie polega na analizie względnych położeń i prędkości statku w stosunku do Ziemi, przy użyciu transformacji Lorentza i podstawowej trygonometrii.