Twoim zadaniem jest narysowanie w jednym czasoprzestrzennym układzie współrzędnych trajektorie obu kul.

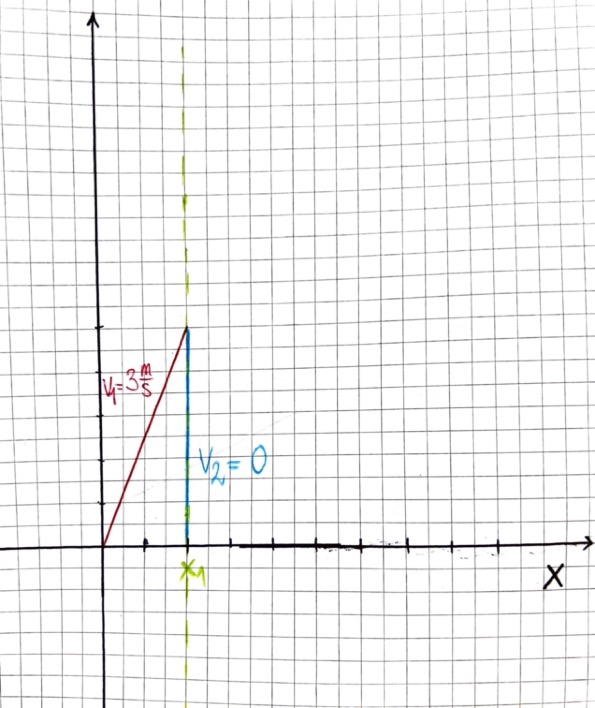
Pierwszy krok polega na narysowaniu układu współrzędnych, gdzie oś $\text{[math]}$ odpowiada osi $\text{[math]}$ . Załóż, że na początku pierwsza kula jest w spoczynku w punkcie $\text{[math]}$ , a druga kula znajduje się w pewnym punkcie $\text{[math]}$ . Następnie, na początku, oznacza punkt początkowy tego układu i narysuj symboliczną prostą, która reprezentuje spoczynek drugiej kuli.

Krok drugi zakłada, że pierwsza metalowa kula toczy się ze stałą prędkością $\text{[math]}$ i przesuwa się w pewnym czasie $\text{[math]}$ w kierunku punktu $\text{[math]}$ , gdzie nadal druga kula pozostaje w spoczynku. Warto zauważyć, że prędkość tej kuli jest bardzo mała w porównaniu z prędkością światła, więc nachylenie tej trajektorii będzie bardzo małe w skali 1:1. Dlatego też dostosowujesz skalę, aby Twój rysunek był czytelny. W tym przypadku trajektoria ruchu pierwszej kuli i spoczynek drugiej kuli wyglądają tak:

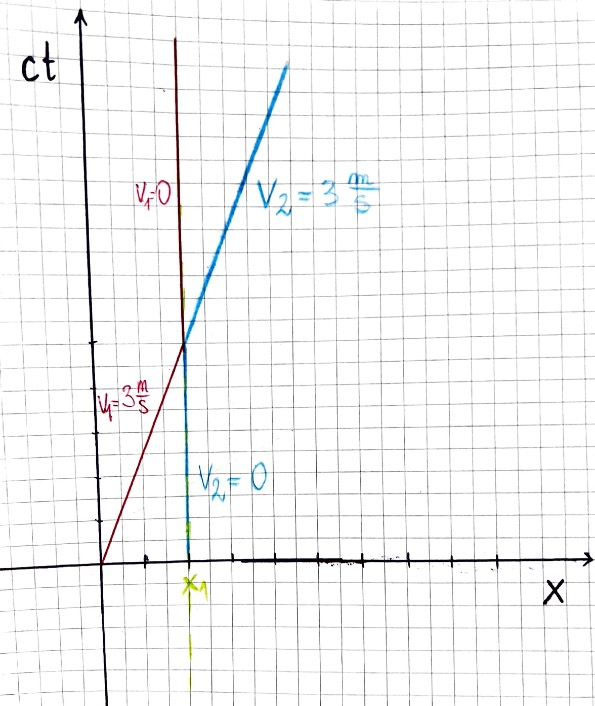
W trzecim etapie Twojego rysunku kulki zderzają się w taki sposób, że pierwsza kula zatrzymuje się w miejscu $\text{[math]}$ , a druga kula zaczyna się poruszać. Zgodnie z zasadą zachowania pędu, jeśli kulki były identyczne, to druga kula kontynuuje ruch z tą samą prędkością, którą poruszała się pierwsza. Oznacza to, że w punkcie $\text{[math]}$ pierwsza kula jest w spoczynku, a druga kula porusza się dalej ze stałą prędkością. W ten sposób zyskujesz ostateczny rysunek, gdzie:

Aby narysować trajektorie obu kul w jednym czasoprzestrzennym układzie współrzędnych, możesz postępować zgodnie z poniższymi krokami:

1. Wybierz odpowiedni arkusz papieru lub kartkę w kratkę, która ułatwi narysowanie trajektorii na skali.

2. Zaznacz na arkuszu punkt początkowy, który będzie reprezentował pozycję pierwszej kuli na początku ruchu. Oznacz ten punkt jako "A" i umieść go w lewym dolnym rogu kartki.

3. Oznacz na kartce kierunek ruchu pierwszej kuli, czyli w prawo, i narysuj strzałkę wskazującą ten kierunek.

4. Następnie narysuj drugą kulę, reprezentując ją jako okrąg. Umieść ją na arkuszu w pewnej odległości od punktu "A". Ta odległość reprezentuje trasę, którą pierwsza kula przebyła przed zderzeniem.

5. Oznacz punkt zderzenia jako "B" i zaznacz go na trajektorii drugiej kuli. Możesz również użyć strzałki, aby wskazać kierunek ruchu drugiej kuli po zderzeniu.

6. Teraz, aby przedstawić, że pierwsza kula zatrzymała się po zderzeniu, narysuj linię prostopadłą do trajektorii pierwszej kuli w punkcie "B". Ta linia reprezentuje zatrzymanie pierwszej kuli.

7. Narysuj trajektorię drugiej kuli po zderzeniu, kontynuując ją od punktu "B" w odpowiednim kierunku, zgodnie z jej prędkością po zderzeniu.

8. Oznacz osie współrzędnych, np. oś x i oś t (czas), aby zrozumieć orientację trajektorii.

9. Uzupełnij rysunek o wszystkie niezbędne oznaczenia, takie jak strzałki wskazujące kierunki ruchu i etykiety punktów A i B.

10. Upewnij się, że rysunek jest czytelny i dokładny, a trajektorie obu kul są wyraźnie widoczne.

To powinno pomóc ci stworzyć czasoprzestrzenny układ współrzędnych z trajektoriami dwóch kul, reprezentując ich ruch przed i po zderzeniu.