DANE:
![]()
![]()
![]()
SZUKANE:
![]()
WZÓR:
Wyznaczamy stosunek odchyleń obu cząstek:
![]()
![]()
![]()
![]()
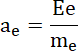
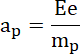
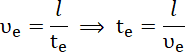
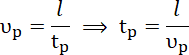
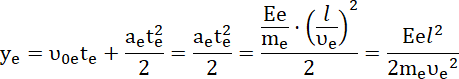
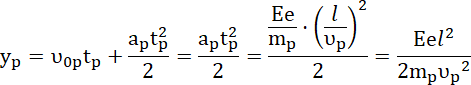
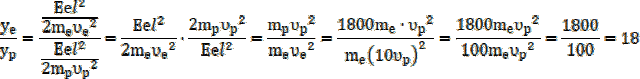

Na obie cząstki naładowane działają sile elektryczne
![]() – dla elektrony i
– dla elektrony i
![]() – dla protonu wzdłuż linii pola jednorodnego powstałego w kondensatorze. Ponieważ mamy do czynienia z tym samym polem jednorodnym, to w obu przypadkach jego natężenie ma tę samą wartość
– dla protonu wzdłuż linii pola jednorodnego powstałego w kondensatorze. Ponieważ mamy do czynienia z tym samym polem jednorodnym, to w obu przypadkach jego natężenie ma tę samą wartość
![]() .
.
Te same siły powodują ruch ze stałym przyspieszeniem, które wyznacz ze wzoru
![]() , gdzie
, gdzie
![]() - siła elektrostatyczna (obliczana jako
- siła elektrostatyczna (obliczana jako
![]() ),
),
![]() – masa cząstki (dla protonu i elektronu). Obie z nich mają ten sam ładunek elementarny
– masa cząstki (dla protonu i elektronu). Obie z nich mają ten sam ładunek elementarny
![]() (różnią się tylko znakiem).
(różnią się tylko znakiem).
Ruch naładowanej cząstki w jednorodnym polu elektrostatycznym rozpatrz jako złożenie dwóch ruchów – równolegle i prostopadle do linii sił pola. Co do ruchu w prostopadłego prędkość składowa (odpowiednio
![]() oraz
oraz
![]() ) nie ulega zmianie, czyli ruch ten jest jednostajny. Z zależności
) nie ulega zmianie, czyli ruch ten jest jednostajny. Z zależności
![]() , gdzie
, gdzie
![]() – przebyta droga (równa długości płytki),
– przebyta droga (równa długości płytki),
![]() - czas ruchu (do momentu opuszczenia pola) wyznacz ich czasy.
- czas ruchu (do momentu opuszczenia pola) wyznacz ich czasy.
Odchylenie
![]() jest równe pokonanej drodze w ruchu jednostajnie przyspieszonym (równolegle do linii pola), którą wyznacz ze wzoru
jest równe pokonanej drodze w ruchu jednostajnie przyspieszonym (równolegle do linii pola), którą wyznacz ze wzoru
![]() , gdzie
, gdzie
![]() – początkowa wartość składowej równoległej prędkości (równa zeru w obu przypadkach). Następnie wyznacz stosunek odchyleń obu cząstek.
– początkowa wartość składowej równoległej prędkości (równa zeru w obu przypadkach). Następnie wyznacz stosunek odchyleń obu cząstek.