W tym zadaniu musisz znaleźć takie wartości parametru p, dla których równanie
![]() ma dwa rozwiązania mniejsze od 3, korzystając z własności wyróżnika
ma dwa rozwiązania mniejsze od 3, korzystając z własności wyróżnika
![]() .
.
Mamy dwa warunki:
Dwa rozwiązania:
![]()
Większe miejscezerowe mniejsze od 3
2)
![]()
Delta:
![]()
![]()
![]()
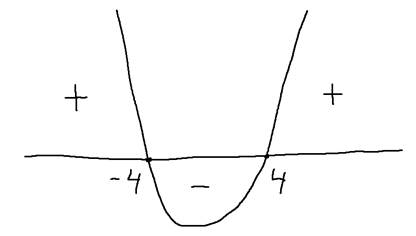
Miejsca zerowe delty:
![]()
![]()
Warunek z miejscamizerowymi
![]()
![]()
![]()
Musimy założyć, że lewa strona jest dodatnia, skoro ma być większa od pierwiastka wtedy rozwiązujemy nierówność w przedziale
![]()
![]()
![]()
![]()
Wynik zgodny z przedziałem
Część wspólna obu warunków:
![]()

Żeby równanie miało dwa miejsca zerowe to delta musi być dodatnia, stąd pierwszy warunek. Żeby oba miejsca zerowe były mniejsze od 3, to większe musi być mniejsze od 3 to drugie automatycznie też będzie. Warto nadmienić, że jeśli współczynnik kierunkowy jest dodatni to
![]() jest większym miejscem zerowym, jeżeli ujemny to
jest większym miejscem zerowym, jeżeli ujemny to
![]() .
.

Ćwiczenie C.
237Zadanie 3.
239Zadanie 4.
239Zadanie 6.
240Zadanie 7.
240Ćwiczenie 8.
240Zadanie 9.
240Zadanie 10.
240Zadanie 11.
240Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 4.
246Zadanie 5.
246Zadanie 7.
246Zadanie 8.
246Zadanie 9.
246Zadanie 10.
246Zadanie 11.
242Ćwiczenie D.
248Zadanie 1.
249Zadanie 2.
249Zadanie 3.
250Zadanie 4.
250Zadanie 5.
250Zadanie A.
252Ćwiczenie B.
253Ćwiczenie C.
254Zadanie 1.
254Zadanie 2.
254Zadanie 3.
254Zadanie 4.
255Zadanie 5.
255Zadanie 7.
255Zadanie 8.
255Zadanie 10.
256Zadanie 11.
256Zadanie 12.
256Zadanie 13.
256Ćwiczenie A.
257Zadanie 1.
259Zadanie 2.
259Zadanie 3.
259Zadanie 4.
259Zadanie 5.
260Zadanie 6.
260Zadanie 7.
260Zadanie 8.
260Zadanie 9.
260Zadanie 12.
260Zadanie 15.
261Zadanie 1.
263Zadanie 2.
263Zadanie 3.
264Zadanie 4.
264Zadanie 5.
264Zadanie 1.
269Zadanie 2.
270Zadanie 3.
270Zadanie 4.
270Zadanie 6.
270Zadanie 7.
270Zadanie 8.
270Zadanie 10.
271Zadanie 11.
271Zadanie 14.
271Zadanie 15.
271Zadanie 17.
271Zadanie 18.
271Zadanie 19.
272Zadanie 20.
272Zadanie 25.
272Zadanie 2.
274Zadanie 3.
274Zadanie 4.
274Zadanie 5.
274Zadanie 9.
274Zadanie 10.
274
