W tym zadaniu musisz znaleźć funkcję
![]() , czyli pola trapezu w zależności od parametru
, czyli pola trapezu w zależności od parametru
![]() .
.
Wzór napole trapezu:
![]()
Gdzie:
![]()
![]()
![]()
![]()
Górna podstawa ma stałą wartość i jest to wartość funkcji w 1
![]()
![]()
Wysokość jest równa
![]() ponieważ jest to odległość argumentu
ponieważ jest to odległość argumentu
![]() od
od
![]() ale możemy pominąć wartość bezwzględną, ponieważ
ale możemy pominąć wartość bezwzględną, ponieważ
![]()
![]() -1
-1
Dolna podstawa to odległość punktu
![]() od osi
od osi
![]() czyli
czyli
![]() ale możemy pominąć wartość bezwzględną, ponieważ
ale możemy pominąć wartość bezwzględną, ponieważ
![]()
![]()
Wstawiamy wszystko do wzoru
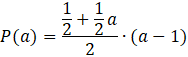
![]()
![]()
![]()
![]()
Pole ma być większe od 6 i mniejsze od 12 rozwiązujemy zestaw nierówności
![]() :
:
Pierwsza nierówność
![]()
![]()
![]()
Ramiona skierowane w górę
Miejsca zerowe:
![]()
![]()
![]()
![]()
![]()
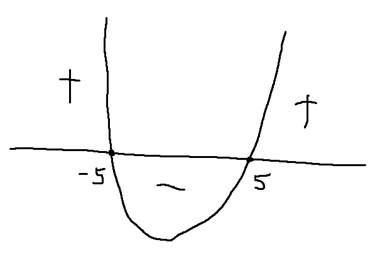
![]()
Uwzględniamy dziedzinę
![]()
![]()
Druga nierówność
![]()
![]()
![]()
Ramiona skierowane w górę
Miejscazerowe:
![]()
![]()
![]()
![]()
![]()
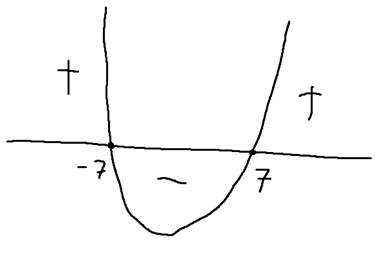
![]()
Uwzględniamy dziedzinę
![]()
![]()
Część wspólna obu zbiorów
![]()
Odpowiedź B

W tym zadaniu trzeba było wszystkie trzy wartości obecne we wzorze na pole trapezu uzależnić od parametru
![]() . Jak już mieliśmy funkcję pola
. Jak już mieliśmy funkcję pola
![]() to rozwiązaliśmy nierówność, aby spełnić warunek podany w treści zadania.
to rozwiązaliśmy nierówność, aby spełnić warunek podany w treści zadania.

Ćwiczenie C.
237Zadanie 3.
239Zadanie 4.
239Zadanie 6.
240Zadanie 7.
240Ćwiczenie 8.
240Zadanie 9.
240Zadanie 10.
240Zadanie 11.
240Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 4.
246Zadanie 5.
246Zadanie 7.
246Zadanie 8.
246Zadanie 9.
246Zadanie 10.
246Zadanie 11.
242Ćwiczenie D.
248Zadanie 1.
249Zadanie 2.
249Zadanie 3.
250Zadanie 4.
250Zadanie 5.
250Zadanie A.
252Ćwiczenie B.
253Ćwiczenie C.
254Zadanie 1.
254Zadanie 2.
254Zadanie 3.
254Zadanie 4.
255Zadanie 5.
255Zadanie 7.
255Zadanie 8.
255Zadanie 10.
256Zadanie 11.
256Zadanie 12.
256Zadanie 13.
256Ćwiczenie A.
257Zadanie 1.
259Zadanie 2.
259Zadanie 3.
259Zadanie 4.
259Zadanie 5.
260Zadanie 6.
260Zadanie 7.
260Zadanie 8.
260Zadanie 9.
260Zadanie 12.
260Zadanie 15.
261Zadanie 1.
263Zadanie 2.
263Zadanie 3.
264Zadanie 4.
264Zadanie 5.
264Zadanie 1.
269Zadanie 2.
270Zadanie 3.
270Zadanie 4.
270Zadanie 6.
270Zadanie 7.
270Zadanie 8.
270Zadanie 10.
271Zadanie 11.
271Zadanie 14.
271Zadanie 15.
271Zadanie 17.
271Zadanie 18.
271Zadanie 19.
272Zadanie 20.
272Zadanie 25.
272Zadanie 2.
274Zadanie 3.
274Zadanie 4.
274Zadanie 5.
274Zadanie 9.
274Zadanie 10.
274
