W ostrosłupie prawidłowym czworokątnym ABCDE, kąt EBF ma miarę 45° (patrz rysunek). Objętość tego ostrosłupa wynosi
![]() . Oblicz, jaka jest wysokość tego ostrosłupa.
. Oblicz, jaka jest wysokość tego ostrosłupa.
H – wysokość ostrosłupa
a – długość krawędzi podstawy
FB = EF = H
![]()
![]()
![]()
![]()
![]()
![]()
![]()
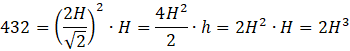
![]()
![]()
![]()
Odp. Wysokość ma 6 cm.

Zauważ, że odcinek EF jest równy wysokości ostrosłupa i długości odcinka EB. Długość odcinka FB jest równa połowie długości przekątnej kwadratu ABCD. Przyrównaj do siebie długość H i połowę długości przekątnej podstawy, czyli
![]() . Wyznacz długość a w zależności od H. Kolejno znając objętość ostrosłupa, wykorzystaj wzór na objętość i wylicz wartość H.
. Wyznacz długość a w zależności od H. Kolejno znając objętość ostrosłupa, wykorzystaj wzór na objętość i wylicz wartość H.

Zadanie 4.
86Zadanie 10.
87Zadanie 11.
87Zadanie 12.
87Zadanie 16.
145Zadanie 22.
88Zadanie 1.
89Zadanie 24.
91Zadanie 1.
92Zadanie 9.
93Zadanie 17.
94Zadanie 19.
94Zadanie 22.
94Zadanie 24.
94Zadanie 1.
95Zadanie 2.
95Zadanie 3.
95Zadanie 4.
95Zadanie 6.
95Zadanie 7.
95Zadanie 12.
96Zadanie 14.
96Zadanie 20.
97Zadanie 25.
97Zadanie 5.
98Zadanie 6.
98Zadanie 5.
101Zadanie 6.
101Zadanie 16.
102Zadanie 26.
103Zadanie 12.
105Zadanie 4.
107Zadanie 7.
107Zadanie 11.
108Zadanie 17.
109Zadanie 15.
111Zadanie 16.
111Zadanie 21.
112Zadanie 24.
112Zadanie 25.
112
