Oblicz pole trójkąta, wiedząc, że obwód jest równy 18, a wysokość opuszczona na podstawę jest o 1 dłuższa od długości tej podstawy.
a – długość podstawy
b – długość ramienia
a+1 wysokość
![]()
![]()
![]()
Z twierdzenia Pitagorasa:
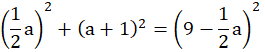
![]()
![]()
![]()
![]()
![]()
Długość podstawy musi być wartością dodatnią zatem a = 5
![]()
Pole trójkąta wynosi 15

Oznacz sobie jako:
a – długość podstawy
b – długość ramienia
a+1 – wysokość
Następnie korzystając ze wzoru na obwód trójkąta, uzależniamy długość ramienia b od długości podstawy a.
![]()
![]()
![]()
Z twierdzenia Pitagorasa dla trójkąta składającego się z wysokości, połowy podstawy trójkąta (są to przyprostokątne) oraz ramienia trójkąta (przeciwprostokątna) oblicz długość podstawy a. Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
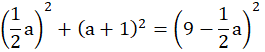
![]()
![]()
Aby obliczyć pierwiastki równania kwadratowego, skorzystaj ze wzoru na deltę:
![]()
![]()
Następnie ze wzorów oblicz pierwiastki równania:
![]()
lub
![]()
Długość podstawy musi być wartością dodatnią zatem a = 5.
Znając wszystkie dane oblicz pole trójkąta równoramiennego.
![]()
Pole trójkąta wynosi 15.

Zadanie 1
55Zadanie 4
55Zadanie 5
55Zadanie 6
55Zadanie 7
56Zadanie 8
56Zadanie 9
56Zadanie 12
56Zadanie 15
57Zadanie 17
57Zadanie 18
57Zadanie 19
57Zadanie 20
58Ćwiczenie A
59Zadanie 1
60Zadanie 2
60Zadanie 3
60Zadanie 4
60Zadanie 6
60Zadanie 8
60Zadanie 10
61Ćwiczenie A
64Zadanie D
64Zadanie 1
66Zadanie 2
66Zadanie 5
66Zadanie 9
66Zadanie 10
67Zadanie 12
66Zadanie 15
66Zadanie 19
67Zadanie 20
67Zadanie 22
67Ćwiczenie A
70Zadanie 1
76Zadanie 8
77Zadanie 19
79Zadanie 21
79Zadanie 22
79Zadanie 27
80Zadanie 29
80Ćwiczenie D
82Zadanie 1
84Zadanie 3
85Zadanie 11
85Zadanie 14
86Zadanie 17
87Zadanie 19
87
