W tym zadaniu policz pole zacieniowanej figury, wiedząc, że w kwadracie o polu 4 połączono każdy wierzchołek ze środkiem jednego z boków – tak jak na rysunku.
![]()
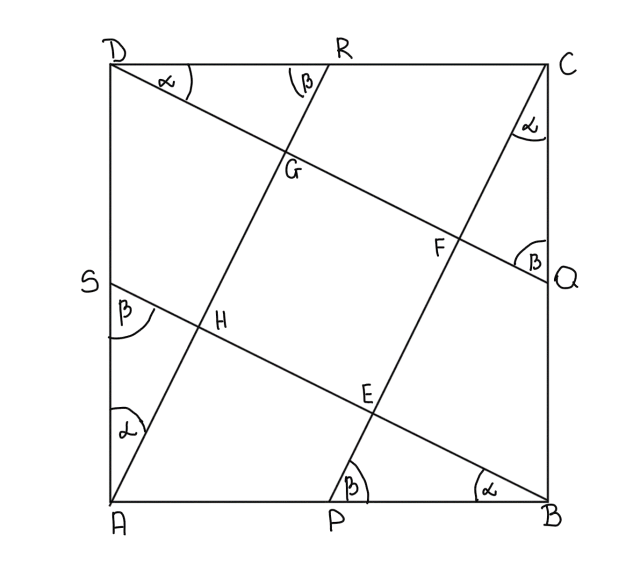
Punkty P, Q, R, S są środkami boków kwadratu ABCD
![]()
Zatem trójkąty PBE, QCF, RDG, SAH są przystające na podstawie cechy KBK
![]()
Kąty PEB i FEH, QFC i GFE, RGD i HGF, SHA i EHG – wierzchołkowe, mają równe miary.
![]()
Czworokąt EFGH jest prostokątem.
Z przystawania trójkątów ABS, BCP, CDQ i DAR oraz PBE, QCF, RDG, SAH
|EF| = |FG| = |GH| = |HE| = |BS|– (|SH|+|EB|)
Prostokąt EFGH jest kwadratem
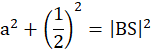
![]()
![]()
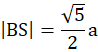
![]()
![]()
Trójkąty ABS i PBE podobne (kkk)
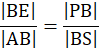
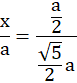
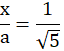
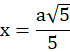
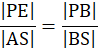

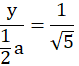
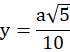
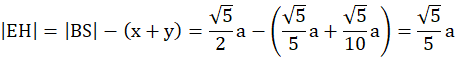
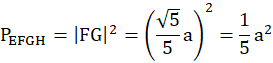
![]()

Skorzystaj z podobieństwa trójkątów
Oblicz długości wszystkich krawędzi
Oblicz pole czworokąta
Przyjmij oznaczenia jak na rysunku:

Zadanie 1
55Zadanie 4
55Zadanie 5
55Zadanie 6
55Zadanie 7
56Zadanie 8
56Zadanie 9
56Zadanie 12
56Zadanie 15
57Zadanie 17
57Zadanie 18
57Zadanie 19
57Zadanie 20
58Ćwiczenie A
59Zadanie 1
60Zadanie 2
60Zadanie 3
60Zadanie 4
60Zadanie 6
60Zadanie 8
60Zadanie 10
61Ćwiczenie A
64Zadanie D
64Zadanie 1
66Zadanie 2
66Zadanie 5
66Zadanie 9
66Zadanie 10
67Zadanie 12
66Zadanie 15
66Zadanie 19
67Zadanie 20
67Zadanie 22
67Ćwiczenie A
70Zadanie 1
76Zadanie 8
77Zadanie 19
79Zadanie 21
79Zadanie 22
79Zadanie 27
80Zadanie 29
80Ćwiczenie D
82Zadanie 1
84Zadanie 3
85Zadanie 11
85Zadanie 14
86Zadanie 17
87Zadanie 19
87
