Dane jest równanie
![]() . Wyznacz wartości parametru 𝑎, dla którego to równanie ma dokładnie jedno rozwiązanie.
. Wyznacz wartości parametru 𝑎, dla którego to równanie ma dokładnie jedno rozwiązanie.
Zauważ, że lewa strona równania to pewien szereg geometryczny. Jego wyraz początkowy to
![]() , natomiast jego iloraz jest równy:
, natomiast jego iloraz jest równy:
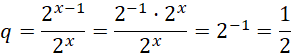
Szereg ten zawsze jest zbieżny.
Korzystając z pozyskanych danych, wyznacz postać jawną tego szeregu:
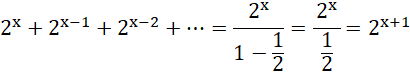
Mamy więc:
![]()
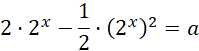
Wprowadź zmienną pomocniczą:
![]()
Mamy więc:
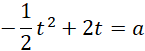
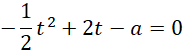
Warunkiem wystarczającym, żeby równanie kwadratowe miało dokładnie jedno rozwiązanie, jest wyróżnik równy zeru. Jako że „zmienna” w równaniu kwadratowym to funkcja wykładnicza, należy zadbać o to, żeby to rozwiązanie było dodatnie. Skorzystaj w tym celu ze wzorów Viete’a:
![]()
Jest również możliwa druga sytuacja: równanie kwadratowe ma dwa rozwiązania o różnych znakach. Wtedy, jako że zmienna 𝑡 przyjmuje wyłącznie wartości większe od zera, tylko jedno rozwiązanie w 𝑡 da rozwiązanie w 𝑥. Drugi zestaw warunków przyjmuje więc postać:
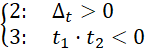
W trzecim przypadku wśród dwóch rozwiązań jedno jest zerem. Wtedy, jako że zmienna 𝑡 przyjmuje wyłącznie wartości większe od zera, tylko jedno rozwiązanie w 𝑡 da rozwiązanie w 𝑥:
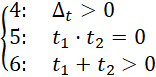
![]()
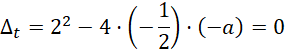
![]()
![]()
Sprawdź, czy rozwiązania dla tego parametru spełniają warunki zadania:
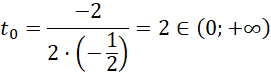
![]()
![]()
Skorzystaj z obliczeń z powyższego podpunktu:
![]()
![]()
![]()
![]()
![]()
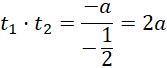
![]()
![]()
![]()
![]()
Skorzystaj z obliczeń z powyższego podpunktu:
![]()
![]()
![]()
![]()
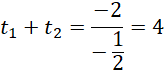
![]()
Wyznacz zbiór rozwiązań:
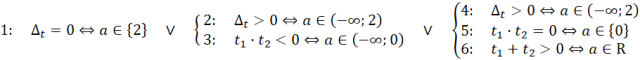
![]()
![]()
![]()
Odp.:
![]() .
.

Zauważ, że lewa strona równania to pewien szereg geometryczny. Skorzystaj ze wzoru na sumę zbieżnego szeregu geometrycznego:
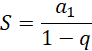
gdzie
![]() to wyraz początkowy ciągu, a
to wyraz początkowy ciągu, a
![]() – iloraz ciągu.
– iloraz ciągu.
Zauważ, że otrzymane równanie to równanie kwadratowe z parametrem. Zastąp funkcję wykładniczą zmienną pomocniczą, a następnie wyznacz wartości 𝑎, dla których wyróżnik wielomianu jest równy zeru oraz miejsce zerowe wielomianu jest dodatnie, lub dla których wyróżnik jest większy bądź równy zeru i dokładnie jedno z rozwiązań jest dodatnie. Skorzystaj w tym celu ze wzoru Viete’a:
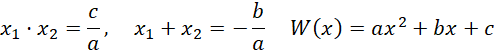
Rozwiąż wynikowe nierówności liniowe.

Zadanie 1.1.
5Zadanie 1.2.
5Zadanie 1.3.
5Zadanie 1.4.
5Zadanie 1.5.
6Zadanie 1.6.
6Zadanie 1.8.
6Zadanie 1.9.
6Zadanie 1.10.
6Zadanie 1.11.
7Zadanie 1.12.
7Zadanie 1.13.
7Zadanie 1.14.
7Zadanie 1.15.
8Zadanie 1.16.
8Zadanie 1.17.
8Zadanie 1.21.
9Zadanie 1.23.
9Zadanie 1.25.
22Zadanie 1.26.
9Zadanie 1.27.
10Zadanie 1.28.
10Zadanie 1.29.
10Zadanie 1.30.
10Zadanie 1.31.
10Zadanie 1.32.
11Zadanie 1.33.
11Zadanie 1.34.
11Zadanie 1.35.
11Zadanie 1.38.
11Zadanie 1.39.
12Zadanie 1.41.
12Zadanie 1.42.
12Zadanie 1.43.
13Zadanie 1.44.
13Zadanie 1.45.
13Zadanie 1.46.
13Zadanie 1.47.
13Zadanie 1.48.
14Zadanie 1.49.
14Zadanie 1.50.
14Zadanie 1.51.
14Zadanie 1.52.
14Zadanie 1.53.
14Zadanie 1.54.
15Zadanie 1.55.
15Zadanie 1.56.
15Zadanie 1.57.
15Zadanie 1.58.
15Zadanie 1.59.
15Zadanie 1.60.
15Zadanie 1.61.
16Zadanie 1.62.
16Zadanie 1.63.
16Zadanie 1.64.
16Zadanie 1.65.
16Zadanie 1.66.
17Zadanie 1.67.
17Zadanie 1.68.
17Zadanie 1.69.
17Zadanie 1.70.
17Zadanie 1.71.
17Zadanie 1.72.
18Zadanie 1.73.
18Zadanie 1.74.
18Zadanie 1.75.
18Zadanie 1.76.
18Zadanie 1.77.
18Zadanie 1.78.
18Zadanie 1.79.
18Zadanie 1.80.
19Zadanie 1.81.
19Zadanie 1.82.
19Zadanie 1.83.
19Zadanie 1.84.
19Zadanie 1.85.
20Zadanie 1.86.
20Zadanie 1.87.
20Zadanie 1.88.
20Zadanie 1.89.
20Zadanie 1.91.
20Zadanie 1.92.
21Zadanie 1.93.
21Zadanie 1.94.
21Zadanie 1.95.
21Zadanie 1.96.
21Zadanie 1.101.
22Zadanie 1.102.
22Zadanie 1.103.
22Zadanie 1.104.
22Zadanie 1.105.
22Zadanie 1.108.
23Zadanie 1.109.
23Zadanie 1.110.
23Zadanie 11.
25Zadanie 19.
26Zadanie 20.
26Zadanie 21.
26Zadanie 22.
26Zadanie 23.
26Zadanie 24.
27Zadanie 25.
27Zadanie 26.
27Zadanie 27.
27Zadanie 28.
27Zadanie 32.
28Zadanie 34.
28Zadanie 35.
28
