Marcin zdał wszystkie egzaminy w sesji zimowej i chciał zaprosić 3 koleżanki i 3 kolegów z grupy do klubu studenckiego. Aby wyrównać proporcje między liczbą studentów i liczbą studentek odwiedzających ten klub, zachęcano dziewczęta niższą ceną biletów. Marcin za bilety dla wszystkich zapłaciłby 122 zł, uznał jednak, że absolutnie nie może wydać na imprezę więcej niż 120 zł. Postanowił zmienić plany. Zaprosił tylko najbliższego przyjaciela, ale za to aż 5 koleżanek. Teraz miał zapłacić tylko 110 zł. Wyznacz cenę w zł biletów do tego klubu dla studentów oraz studentek.
Ustalamy zmienne:
![]() – cena biletów dla studentów w zł,
– cena biletów dla studentów w zł,
![]() – cena biletów dla studentek w zł.
– cena biletów dla studentek w zł.
Marcin chciał zaprosić 3 koleżanki i 3 kolegów i zapłaciłby 122 zł, czyli:
![]()
ponieważ płaci też za siebie.
Zaprosił tylko najbliższego przyjaciela, ale za to aż 5 koleżanek i miał zapłacić tylko 110 zł, czyli:
![]()
ponieważ płaci też za siebie.
Układamy układ równań:
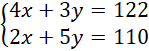
Rozwiązujemy układ równań metodą przeciwnych współczynników:
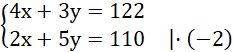
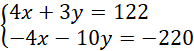
Dodajemy równania stronami i układamy równoważny układ równań:
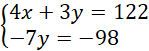
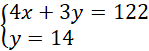
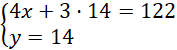
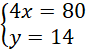
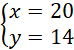
Odp. Bilety dla studentów kosztują 20 zł, a dla studentek 14 zł.

Niektóre problemy wygodnie jest zapisywać w postaci układu równań. Przyjmujemy szukane wartości jako niewiadome, a następnie zawieramy relacje zawarte w zadaniu jako równania liniowe dwóch zmiennych.
W metodzie przeciwnych współczynników wykonujemy prosty algorytm, by znaleźć rozwiązanie danego układu równań:
1. Sprawdzamy, czy przy którejś niewiadomej występują przeciwne współczynniki. Jeżeli nie, to przekształcamy równania układu tak, aby otrzymać przeciwne współczynniki.
2. Dodajemy równania stronami.
3. Obliczamy niezredukowaną niewiadomą.
4. Tworzymy nowy układ równań równoważny wyjściowemu.
5. Rozwiązujemy otrzymany układ równań.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
