Dla podanego wyrażenia określ założenia, które są konieczne, aby działania wewnątrz niego były wykonalne. Następnie korzystając z tych założeń przedstaw zbiór liczb, które można podstawiać do wyrażenia w miejsce litery x, oznaczając go literą D.
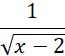
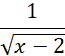
Aby działania w podanym wyrażeniu były wykonalne, muszą zostać spełnione 2 warunki:
1.
Wyrażenie w mianowniku musi być różne od 0.
2.
Wyrażenie pod pierwiastkiem musi być większe lub równe 0.
Jednak, jako że pierwiastek znajduje się w mianowniku ułamka to wyrażenie wewnątrz niego nie może być równe 0, ponieważ:
![]()
Dlatego łącząc oba warunki wychodzi nam, że aby działania w podanym wyrażeniu były wykonalne, to wyrażenie pod pierwiastkiem musi być większe od 0, a więc:
![]()
![]()
Tak więc w miejsce zmiennej x możemy podstawić dowolną liczbę większą od 2, a więc:
![]()

Przeanalizuj podane wyrażenie i określ założenia jakie muszą spełniać liczby wewnątrz niego, aby obecne w nim działania były wykonalne. W tym przypadku liczba x musi być większa od 2, ponieważ gdyby była równa 2 to wyrażenie w mianowniku ułamka byłoby równe 0, a nie można dzielić przez 0, natomiast gdyby była mniejsza od 2 to wyrażenie pod pierwiastkiem byłoby ujemne, a nie można pierwiastkować liczb ujemnych. Na końcu zauważ, że w miejsce zmiennej x można wstawić dowolną liczbę większą od 2 oraz przedstaw to jako zbiór D.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
