Właściciel sklepu z owocami kupił na giełdzie truskawki i czereśnie. Cena hurtowa kilograma czereśni była o 2 zł wyższa niż cena hurtowa kilograma truskawek. Właściciel sklepu ustalił cenę sprzedaży czereśni o 25% wyższą od ceny hurtowej, a cenę sprzedaży truskawek – o 30% wyższą od ceny hurtowej. Za pół kilograma czereśni i kilogram truskawek klient zapłacił w sklepie 8,95 zł. Wyznacz cenę sklepową kilograma truskawek i czereśni.
Ustalamy zmienne:
![]() – cena hurtowa truskawek w złotych,
– cena hurtowa truskawek w złotych,
![]() – cena hurtowa czereśni w złotych.
– cena hurtowa czereśni w złotych.
Cena hurtowa kilograma czereśni była o 2 zł wyższa niż cena hurtowa kilograma truskawek, czyli:
![]()
![]()
Właściciel sklepu ustalił cenę sprzedaży czereśni o 25% wyższą od ceny hurtowej, a cenę sprzedaży truskawek – o 30% wyższą od ceny hurtowej. Za pół kilograma czereśni i kilogram truskawek klient zapłacił w sklepie 8,95 zł, czyli:
![]()
Układamy układ równań:
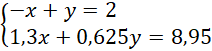
Rozwiązujemy układ równań metodą przeciwnych współczynników:
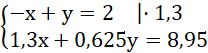
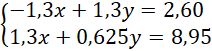
Dodajemy równania stronami i układamy równoważny układ równań:
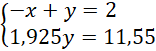
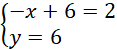
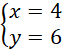
Mnożymy ceny hurtowe przez narzut:
![]()
![]()
Odp. Truskawki kosztują 5,40 zł, a czereśnie 7,50 zł za kilogram.

Niektóre problemy wygodnie jest zapisywać w postaci układu równań. Przyjmujemy szukane wartości jako niewiadome, a następnie zawieramy relacje zawarte w zadaniu jako równania liniowe dwóch zmiennych.
W metodzie przeciwnych współczynników wykonujemy prosty algorytm, by znaleźć rozwiązanie danego układu równań:
1. Sprawdzamy, czy przy którejś niewiadomej występują przeciwne współczynniki. Jeżeli nie, to przekształcamy równania układu tak, aby otrzymać przeciwne współczynniki.
2. Dodajemy równania stronami.
3. Obliczamy niezredukowaną niewiadomą.
4. Tworzymy nowy układ równań równoważny wyjściowemu.
5. Rozwiązujemy otrzymany układ równań.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
