Znajdź rozwiązanie układu równań
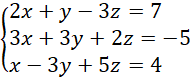 .
.
Nie ma współczynników o przeciwnych znakach, więc przekształcamy układ równań tak, by do takiej sytuacji dochodziło:
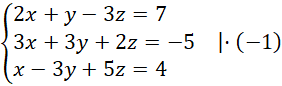
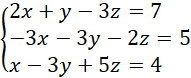
Dodajemy równania stronami i obliczamy wynikowe równanie:
![]()
![]()
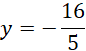
Tworzymy nowy, równoważny układ:
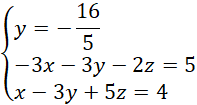
Podstawiamy wyliczone
![]() do drugiego i trzeciego równania:
do drugiego i trzeciego równania:
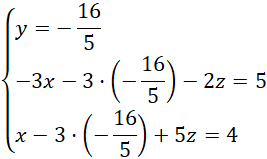
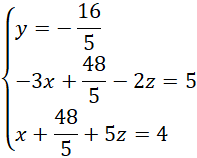
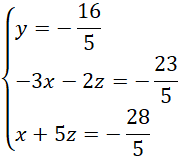
Modyfikujemy układ w taki sposób, by drugie i trzecie równanie miały przeciwne współczynniki:
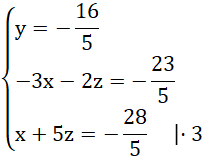
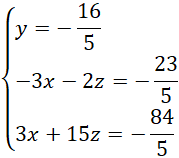
Dodajemy stronami dwa ostatnie równania:
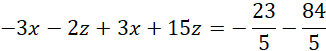
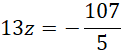
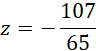
Tworzymy nowy, równoważny układ:
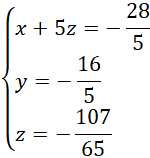
Podstawiamy wartość
![]() do pierwszego równania:
do pierwszego równania:
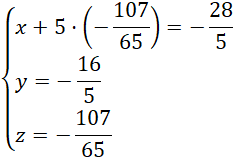
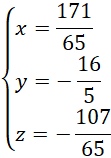
Odp. Rozwiązaniem jest trójka liczb
![]() .
.

W metodzie przeciwnych współczynników wykonujemy prosty algorytm, by znaleźć rozwiązanie danego układu równań:
1. Sprawdzamy, czy przy którejś niewiadomej występują przeciwne współczynniki. Jeżeli nie, to przekształcamy równania układu tak, aby otrzymać przeciwne współczynniki.
2. Dodajemy równania stronami.
3. Obliczamy niezredukowaną niewiadomą.
4. Tworzymy nowy układ równań równoważny wyjściowemu.
5. Rozwiązujemy otrzymany układ równań.
W metodzie podstawiania wykonujemy prosty algorytm, by znaleźć rozwiązanie danego układu równań:
1. Wyznaczamy z jednego równania dowolną niewiadomą.
2. Wstawiamy otrzymane wyrażenie w miejsce wyznaczonej zmiennej w drugim równaniu.
3. Obliczamy drugą zmienną z otrzymanego równania z jedną niewiadomą.
4. Podstawiamy wyznaczoną wartość drugiej zmiennej do jednego z równań układu i obliczamy pierwszą zmienną.
W bardziej skomplikowanych zadaniach nieraz wygodniejsze jest mieszanie powyższych technik niż kurczowe stosowanie jednej.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
