Michał ważył za dużo, więc zaczął zwracać uwagę na to, co je. Na podwieczorek, zamiast dwóch drożdżówek, przygotował sobie trzy kromki chleba graham i 2 szklanki mleka. Kiedy jednak zajrzał do tabeli wartości kalorycznych, przekonał się, że jego podwieczorek to aż 334 kcal. Zredukował go więc do 2 kromek chleba i 1 szklanki mleka. Rezultat był lepszy – tylko 182 kcal. Uspokojony zabrał się do jedzenia. Wyznacz wartość kaloryczną jednej kromki chleba oraz jednej szklanki mleka.
Ustalamy zmienne:
![]() – wartość kaloryczna jednej kromki chleba w kcal,
– wartość kaloryczna jednej kromki chleba w kcal,
![]() – wartość kaloryczna jednej szklanki mleka w kcal.
– wartość kaloryczna jednej szklanki mleka w kcal.
Na podwieczorek przygotował sobie trzy kromki chleba graham i 2 szklanki mleka i przekonał się, że jego podwieczorek to aż 334 kcal, czyli:
![]()
Zredukował go więc do 2 kromek chleba i 1 szklanki mleka. Rezultat był lepszy – tylko 182 kcal, czyli:
![]()
Układamy układ równań:
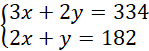
Rozwiązujemy układ równań metodą przeciwnych współczynników:
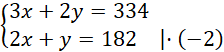
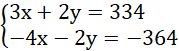
Dodajemy równania stronami i układamy równoważny układ równań:
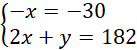
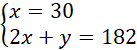
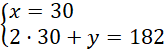
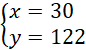
Odp. Kromka chleba ma 30 kcal, a szklanka mleka 122 kcal.

Niektóre problemy wygodnie jest zapisywać w postaci układu równań. Przyjmujemy szukane wartości jako niewiadome, a następnie zawieramy relacje zawarte w zadaniu jako równania liniowe dwóch zmiennych.
W metodzie przeciwnych współczynników wykonujemy prosty algorytm, by znaleźć rozwiązanie danego układu równań:
1. Sprawdzamy, czy przy którejś niewiadomej występują przeciwne współczynniki. Jeżeli nie, to przekształcamy równania układu tak, aby otrzymać przeciwne współczynniki.
2. Dodajemy równania stronami.
3. Obliczamy niezredukowaną niewiadomą.
4. Tworzymy nowy układ równań równoważny wyjściowemu.
5. Rozwiązujemy otrzymany układ równań.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
