Oblicz rozwiązanie równania.
![]()
![]()
Na początku obliczmy dla jakich wartości x wyrażenia w podanych wartościach bezwzględnych są większe lub równe 0.
![]()
![]()
![]()
Zatem pierwsze wyrażenie jest większe lub równe 0 dla x mniejszych lub równych 3, a ujemne dla x większych od 3.
![]()
![]()
![]()
Zatem drugie wyrażenie jest większe lub równe 0 dla x mniejszych lub równych 2, a ujemne dla x większych od 2.
W takim razie opuszczając wartości bezwzględne będziemy musieli rozpatrzeć 3 przypadki we trzech różnych przedziałach:
Pierwszy przypadek:
![]()
W tym przedziale wyrażenia wewnątrz obu wartości bezwzględnych są dodatnie, więc opuszczamy je bez zmiany znaku na przeciwny:
![]()
![]()
![]()
Obliczona wartość x należy do rozpatrywanego przedziału, a więc jest jednym z rozwiązań podanego równania.
Drugi przypadek:
![]()
W tym przedziale wyrażenie wewnątrz pierwszej wartości bezwzględnej jest dodatnie, a wewnątrz drugiej jest ujemne zatem opuszczamy je odpowiednio:
![]()
![]()
Obliczona wartość x nie należy do rozpatrywanego przedziału, a więc nie jest jednym z rozwiązań podanego równania.
Trzeci przypadek:
![]()
W tym przedziale wyrażenia wewnątrz obu wartości bezwzględnych są ujemne, więc opuszczamy je ze zmianą znaku na przeciwny:
![]()
![]()
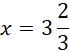
Obliczona wartość x należy do rozpatrywanego przedziału, a więc jest jednym z rozwiązań podanego równania.
W takim razie rozwiązaniem podanego równania są:
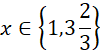

Na początku oblicz przedziały, w których wyrażenia wewnątrz wartości bezwzględnych są dodatnie i ujemne. Zauważ, że przedziały te dzielą zbiór liczb rzeczywistych na 3 części i dla każdej z nich osobno opuść wartości bezwzględne w odpowiedni sposób oraz oblicz rozwiązania tak powstałych równań. Sprawdź czy obliczone rozwiązania zawierają się w danej części zbioru liczb rzeczywistych i jeśli tak, to należą one do zbioru rozwiązań całego równania.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
