Używając podanego warunku, jaki spełnia zmienna x, przedstaw podane wyrażenie bez użycia symbolu wartości bezwzględnej.
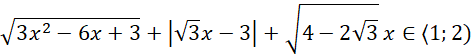
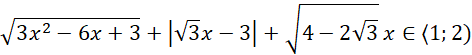
Najpierw przekształćmy to wyrażenie tak, aby pozbyć się dwóch wielkich pierwiastków:
![]()
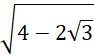
W tym celu musimy zapisać wyrażenie pod pierwiastkiem jako kwadrat jakiegoś wyrażenia. Następnie możemy skrócić kwadrat z pierwiastkiem i zapisać to wyrażenie wewnątrz wartości bezwzględnej, ponieważ:
![]() , dla
, dla
![]()
Zauważ, że wyrażenie pod pierwszym pierwiastkiem można przekształcić przy pomocy wzoru skróconego mnożenia na kwadrat różnicy:
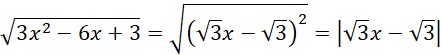
Zauważ też, że wyrażenie pod drugim pierwiastkiem można najpierw rozpisać, a następnie przekształcić przy pomocy wzoru skróconego mnożenia na kwadrat różnicy:
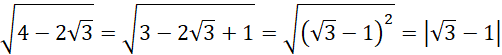
A więc przekształcone wyrażenie wygląda tak:
![]()
Teraz oszacujmy, czy wyrażenia wewnątrz wartości bezwzględnych są dodatnie czy ujemne:
Pierwsze wyrażenie:
Jako że x jest większe lub równe 1, to wartość pierwszego wyrażenia jest większa lub równa 0. Dlatego możemy opuścić wartość bezwzględną bez zmiany znaku.
Drugie wyrażenie:
Tutaj sytuacja jest trochę bardziej skomplikowana. Zmienna x jest większa lub równa 1 i mniejsza od 2. W takiej sytuacji drugie wyrażenie może być zarówno dodatnie jak i ujemne, ponieważ:
![]()
Dlatego w tej sytuacji będziemy mieć dwa przypadki dla dwóch różnych zbiorów wartości x. Zauważmy, że wartością graniczną tutaj jest
![]() , ponieważ wtedy wyrażenie miałoby wartość:
, ponieważ wtedy wyrażenie miałoby wartość:
![]()
Dlatego jeśli x jest mniejsze od
![]() to wyrażenie jest ujemne, a jeśli x jest większe lub równe
to wyrażenie jest ujemne, a jeśli x jest większe lub równe
![]() to wyrażenie jest dodatnie.
to wyrażenie jest dodatnie.
Trzecie wyrażenie:
![]() , ponieważ:
, ponieważ:
![]()
W takim razie trzecie wyrażenie jest dodatnie.
Opuśćmy teraz pierwszą i trzecią wartość bezwzględną:
![]()
Teraz rozpatrzmy dwa przypadki:
Dla
![]() :
:
![]()
Dla
![]() :
:
![]()

Pamiętając definicję wartości bezwzględnej i wynikające z niej zależności oraz znając warunek jaki spełnia zmienna x, przedstaw podane wyrażenie bez symboli wartości bezwzględnej. Zauważ, że możesz wyciągnąć dwa wyrażenia spod pierwiastków przy pomocy wzoru skróconego mnożenia
![]() . Zauważ też, że wyrażenie wewnątrz jednej z wartości bezwzględnych może być zarówno większe lub równe 0, jak i mniejsze od 0, a więc musisz rozpatrzyć te dwa przypadki osobno.
. Zauważ też, że wyrażenie wewnątrz jednej z wartości bezwzględnych może być zarówno większe lub równe 0, jak i mniejsze od 0, a więc musisz rozpatrzyć te dwa przypadki osobno.

Zadanie 1.4.
104Zadanie 1.5.
105Zadanie 1.6.
105Zadanie 1.7.
105Zadanie 1.8.
105Zadanie 1.9.
105Zadanie 2.5.
111Zadanie 2.6.
111Zadanie 2.8.
111Zadanie 2.9.
111Zadanie 2.10.
112Zadanie 2.11.
112Zadanie 2.12.
112Zadanie 3.4.
118Zadanie 3.5.
118Zadanie 3.7.
118Zadanie 3.8.
119Zadanie 3.9.
119Zadanie 3.10.
119Zadanie 3.11.
119Zadanie 3.12.
119Zadanie 3.13.
119Zadanie 3.14.
120Zadanie 4.5.
126Zadanie 4.6.
126Zadanie 4.7.
126Zadanie 4.8.
126Zadanie 4.9.
126Zadanie 4.10.
127Zadanie 4.11.
127Zadanie 4.12.
127Zadanie 4.13.
127Zadanie 4.14.
127Zadanie 4.15.
127Zadanie 5.5.
131Zadanie 5.6.
131Zadanie 5.7.
132Zadanie 5.8.
132Zadanie 5.9.
132Zadanie 5.10.
132Zadanie 5.11.
132Zadanie 5.12.
132Zadanie 5.13.
133Zadanie 5.14.
133Zadanie 5.15.
133Zadanie 6.6.
140Zadanie 6.7.
140Zadanie 6.8.
140Zadanie 6.9.
140Zadanie 6.10.
140Zadanie 6.11.
140Zadanie 6.12.
141Zadanie 6.13.
141Zadanie 6.14.
141Zadanie 6.15.
141Zadanie 6.16.
141Zadanie 6.17.
142Zadanie 6.18.
142Zadanie 7.6.
150Zadanie 7.7.
150Zadanie 7.8.
150Zadanie 7.9.
151Zadanie 7.11.
151Zadanie 7.16.
151Zadanie 7.17.
152Zadanie 7.18.
152Zadanie 7.19.
152Zadanie 7.20.
152Zadanie 7.21.
152Zadanie 7.22.
152Zadanie 7.23.
152Zadanie 7.24.
152Zadanie 7.25.
153Zadanie 7.26.
153Zadanie 8.3.
162Zadanie 8.4.
162Zadanie 8.11.
162Zadanie 8.12.
162Zadanie 8.17.
163Zadanie 8.21.
163Zadanie 8.23.
163Zadanie Prosto do matury 5.
164Zadanie 9.6.
171Zadanie 9.7.
171Zadanie 9.8.
171Zadanie 9.9.
171Zadanie 9.10.
171Zadanie 10.5.
184Zadanie 10.6.
185Zadanie 10.7.
185Zadanie 10.8.
185Zadanie 10.9.
185Zadanie 10.10.
186Zadanie 10.11.
186Zadanie 10.12.
186Zadanie 10.13.
186Zadanie 10.14.
187Zadanie 10.15.
187Zadanie 10.16.
187Zadanie 10.17.
187Zadanie 10.21.
188Zadanie 40.
195Zadanie 43.
195Zadanie 44.
195Zadanie 45.
195Zadanie 65.
197Zadanie 67.
197Zadanie 68.
197Zadanie 69.
197Zadanie 77.
198
