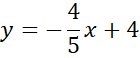Prosta AD:
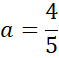
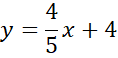
Prosta BC:
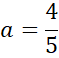
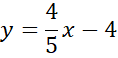
Prosta AB:
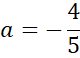
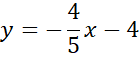
Prosta CD:
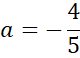
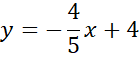
Zapisz wzór na równanie kierunkowe prostej.
Zacznij od wyznaczenia wzoru prostej przechodzącej przez punkty A i D.
Zauważ, że punkt (0,4) jest miejscem przecięcia wykresu szukanej funkcji z osią OY, więc druga współrzędna tego punktu jest równa wyrazowi wolnemu – współczynnikowi
w powyższym wzorze funkcji.
Skorzystaj z tego, że do szukanej prostej należy punkt (-5,0). Podstaw jego współrzędne w miejsce
i
w powyższym równaniu i wyznacz wartość współczynnika
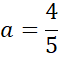
Zapisz wzór prostej AD.
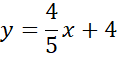
Zauważ, że przeciwległe boki rombu są równoległe, więc proste AD i BC mają takie same współczynniki kierunkowe, a punkt (0,-4) jest miejscem przecięcia wykresu szukanej funkcji z osią OY, więc:
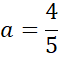
Zapisz wzór prostej BC.
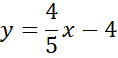
Podobnie postąp ze znalezieniem wzorów funkcji AB i CD.
Zauważ, że punkt (0,-4) jest miejscem przecięcia wykresu szukanej funkcji z osią OY, więc druga współrzędna tego punktu jest równa wyrazowi wolnemu – współczynnikowi
w powyższym wzorze funkcji.
Skorzystaj z tego, że do szukanej prostej należy punkt (-5,0). Podstaw jego współrzędne w miejsce
i
w powyższym równaniu i wyznacz wartość współczynnika
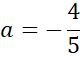
Zapisz wzór prostej AB.
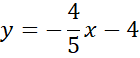
Ponownie zauważ, że przeciwległe boki rombu są równoległe, więc proste AB i CD mają takie same współczynniki kierunkowe, a punkt (0,4) jest miejscem przecięcia wykresu szukanej funkcji z osią OY, więc:
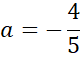
Zapisz wzór prostej CD.
