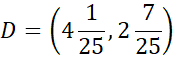
Prosta AB:
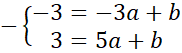
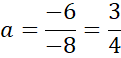
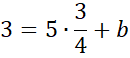
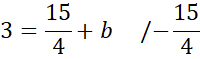
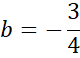
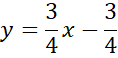
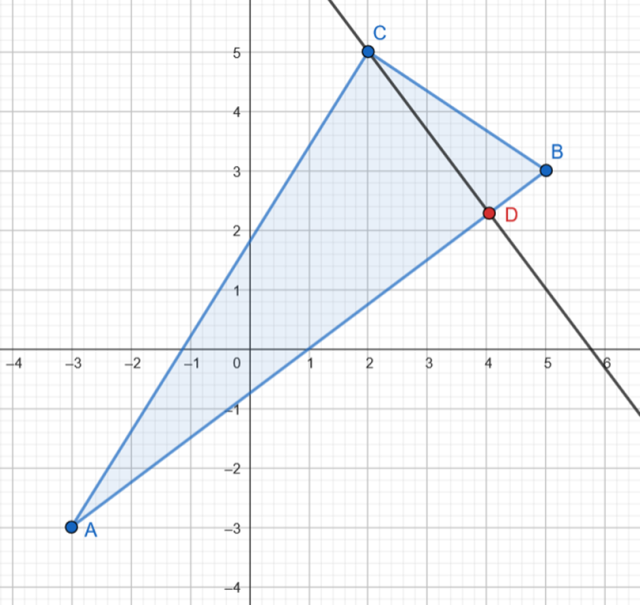
Proste AB i CD są prostopadłe.
Prosta CD:
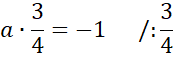
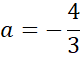
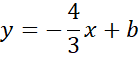
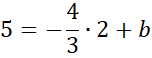
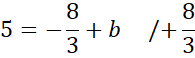
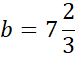
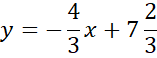
Punkt D:
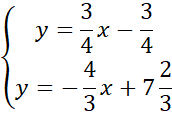
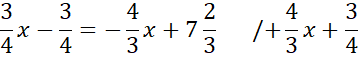
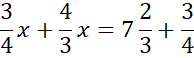
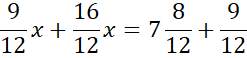
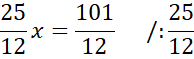
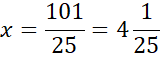
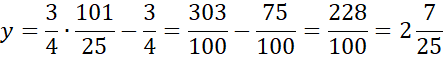
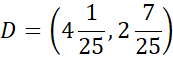
Wprowadź oznaczenia pomocnicze. Jako punkt D oznacz szukany spodek wysokości poprowadzonej z wierzchołka C.
Współrzędne punktów A i B podstaw pod równanie kierunkowe prostej:
. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Wyznacz wartość współczynnika a odejmując od siebie równania stronami.
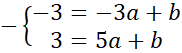
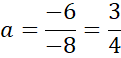
Podstaw wyznaczoną wartość a pod jedno z początkowych równań w powyższym układzie równań i na tej podstawie wyznacz wartość współczynnika b.
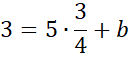
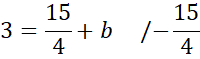
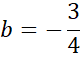
Zapisz równanie prostej AB.
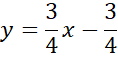
Zauważ, że wysokość opuszczona z wierzchołka C jest prostopadła do boku AB, więc proste AB i CD są prostopadłe, czyli ich współczynniki kierunkowe muszą być przeciwne i odwrotne i spełniać warunek:
Pod powyższe równanie podstaw współczynnik kierunkowy prostej AB i wyznacz wartość współczynnika prostej prostopadłej, czyli prostej CD.
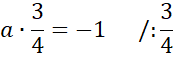
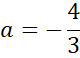
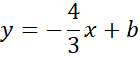
Skorzystaj z tego, że do wykresu prostej CD należy punkt C. Podstaw jego współrzędne w miejsce x i y w powyższym równaniu, aby obliczyć wartość współczynnika b.
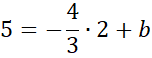
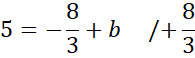
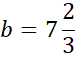
Zapisz wzór prostej CD.
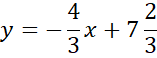
Skorzystaj z tego, że punkt D jest miejscem przecięcia prostych AB i CD. Ponownie zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Porównaj ze sobą wartości y w obu równaniach i na tej podstawie wyznacz wartość x.
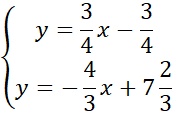
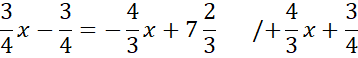
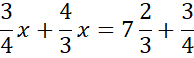
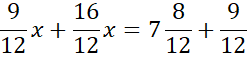
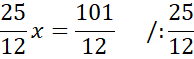
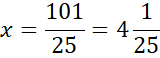
Wyznaczoną wartość x wstaw pod jedno z początkowych równań w powyższym układzie równań i wyznacz wartość y.
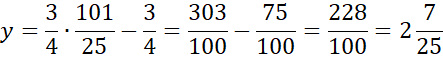
Zapisz współrzędne szukanego punktu.
