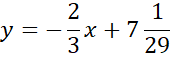
Prosta AB:
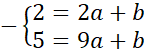
![]()
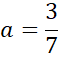
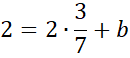
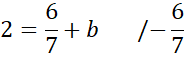
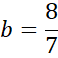
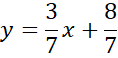
Prosta CD jest prostopadła do prostej AB.
Prosta CD:
![]()
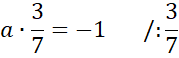
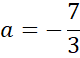
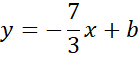
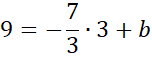
![]()
![]()
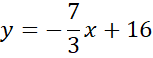
Punkt D:
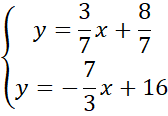
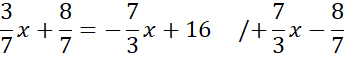
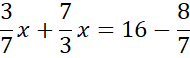
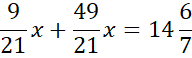
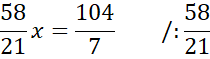
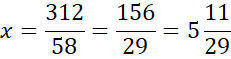
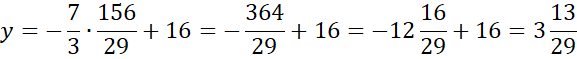
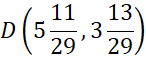
Prosta BC:
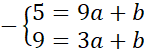
![]()
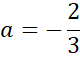
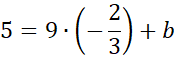
![]()
![]()
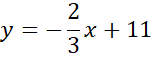
Prosta równoległa do prostej BC przechodząca przez punkt D:
![]()
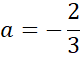
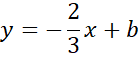
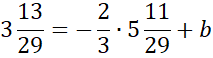
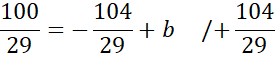
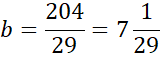
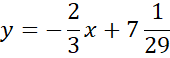

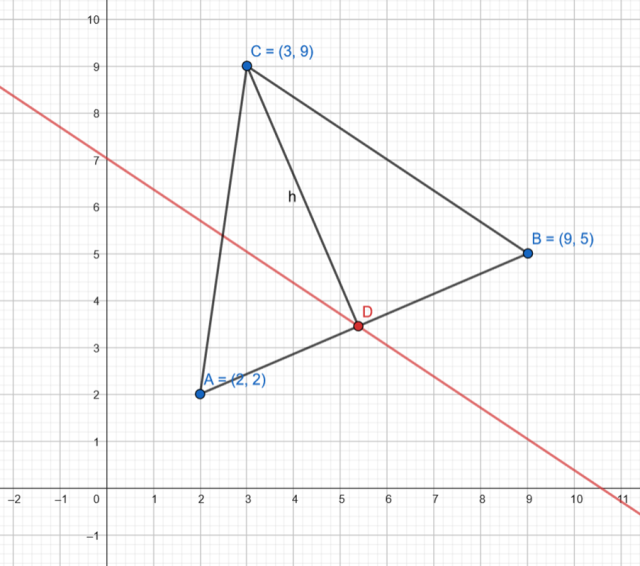
Wprowadź oznaczenia pomocnicze. Jako punkt D oznacz spodek wysokości poprowadzonej z wierzchołka C.
Współrzędne punktów A i B podstaw pod równanie kierunkowe prostej:
![]() . Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Wyznacz wartość współczynnika a odejmując od siebie równania stronami.
. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Wyznacz wartość współczynnika a odejmując od siebie równania stronami.
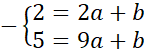
![]()
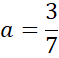
Podstaw wyznaczoną wartość a pod jedno z początkowych równań w powyższym układzie równań i na tej podstawie wyznacz wartość współczynnika b.
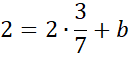
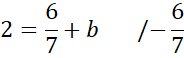
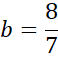
Zapisz równanie prostej AB.
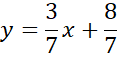
Zauważ, że wysokość opuszczona z wierzchołka C jest prostopadła do boku AB, więc proste AB i CD są prostopadłe, czyli ich współczynniki kierunkowe muszą być przeciwne i odwrotne i spełniać warunek:
![]()
Pod powyższe równanie podstaw współczynnik kierunkowy prostej AB i wyznacz wartość współczynnika prostej prostopadłej, czyli prostej CD.
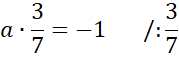
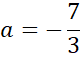
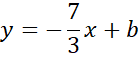
Skorzystaj z tego, że do wykresu prostej CD należy punkt C. Podstaw jego współrzędne w miejsce x i y w powyższym równaniu, aby obliczyć wartość współczynnika b.
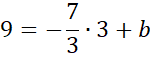
![]()
![]()
Zapisz wzór prostej CD.
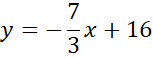
Skorzystaj z tego, że punkt D jest miejscem przecięcia prostych AB i CD. Ponownie zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Porównaj ze sobą wartości y w obu równaniach i na tej podstawie wyznacz wartość x.
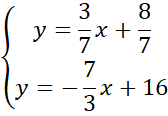
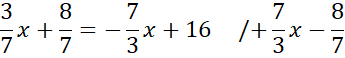
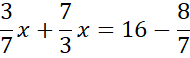
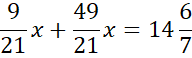
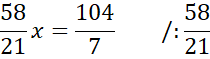
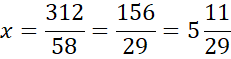
Wyznaczoną wartość x wstaw pod jedno z początkowych równań w powyższym układzie równań i wyznacz wartość y.
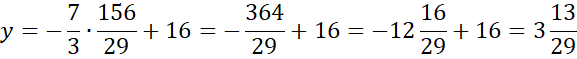
Zapisz współrzędne punktu D.
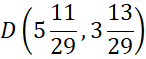
Wyznacz równanie prostej BC, aby to zrobić współrzędne punktów B i C podstaw pod równanie kierunkowe prostej:
![]() . Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Wyznacz wartość współczynnika a odejmując od siebie równania stronami.
. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Wyznacz wartość współczynnika a odejmując od siebie równania stronami.
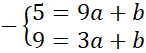
![]()
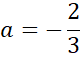
Podstaw wyznaczoną wartość a pod jedno z początkowych równań w powyższym układzie równań i na tej podstawie wyznacz wartość współczynnika b.
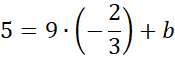
![]()
![]()
Zapisz równanie prostej BC.
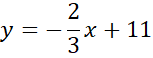
Na koniec pozostało wyznaczyć równanie prostej równoległej do prostej BC przechodząca przez punkt D.
Proste są równoległe, gdy ich wartość stojąca przy
![]() we wzorze funkcji
we wzorze funkcji
![]() jest taka sama. Na tej podstawie zapisz współczynnik kierunkowy szukanej prostej, jeśli jest ona równoległa do prostej BC.
jest taka sama. Na tej podstawie zapisz współczynnik kierunkowy szukanej prostej, jeśli jest ona równoległa do prostej BC.
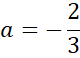
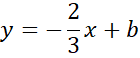
Skorzystaj z tego, że do szukanej prostej należy punkt D. Podstaw jego współrzędne w miejsce
![]() i
i
![]() w powyższym równaniu i wyznacz wartość współczynnika
w powyższym równaniu i wyznacz wartość współczynnika
![]()
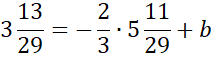
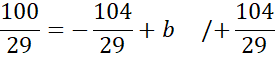
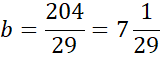
Zapisz równanie szukanej prostej.