x - długość najkrótszego boku
y – długość najdłuższego boku
z – długość trzeciego boku
stosunek 6 : 8 : 10
Stosunek najkrótszego do najdłuższego:
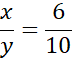
Po mnożeniu na krzyż otrzymujemy:
10x = 6y / :2
5x = 3y / : 5
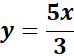
Różnica najdłuższego i nakrótszego boku:
y - x = 8 cm
y = 8 + x
Możemy przyrównać oba wzory na y:
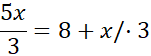
5x = 24 + 3x / - 3x
2x = 24 / : 2
x = 12
y = 8 + x = 8 + 12 = 20
y = 20
Możemy skorzystać z twierdzenia Pitagorasa, aby obliczyć 3 krawędź:
x2 + z2 = y2 / - x2
z2 = y2 - x2
z2 = 202 - 122 = 400 – 144 = 256
z = 16
Obw. = z + x + y = 16 + 12 + 20 = 48 cm
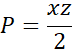
P = 96 cm2
Odp.: Pole wynosi 96 cm2, a obwód 48 cm.

Na podstawie danych z zadania możemy ułożyć proporcję oraz różnicę między dwoma bokami – oba zapisy doprowadzą nas do wzorów na s do wzorów na y, co oznacza, że dadzą ten sam wynik. Możemy je więc ze sobą porównać, aby otrzymać liczbę, która kryje się pod y. Zwróć uwagę na fakt, że jest to trójkąt prostokątny, zatem trzeci bok można obliczyć stosując twierdzenie Pitagorasa.