W tym zadaniu musisz obliczyć wysokość graniastosłupa tak, aby trójkąt zbudowany z przekątnej ściany bocznej, dłuższej przekątnej podstawy i krótszej przekątnej graniastosłupa był równoramienny.
a – krawędź podstawy graniastosłupa
2a – długość dłuższej przekątnej podstawy
d – przekątna ściany bocznej
H – wysokość ostrosłupa
x – krótsza przekątna graniastosłupa
![]()
![]()
![]()
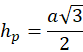
![]()
![]()
Aby trójkąt był równoramienny dwa z trzech boków muszą być równe.
Przekątna ściany bocznej=dłuższa przekątna podstawy
![]()
![]()
![]()
![]()
![]()
Dłuższa przekątna podstawy = krótsza przekątna graniastosłupa
![]()
![]()
![]()
![]()
![]()
Przekątna ściany bocznej=krótsza przekątna graniastosłupa
![]()
![]()
![]()
![]()
![]()

Dłuższa przekątna podstawy graniastosłupa jest równa dwukrotności boku sześciokąta. Przekątną ściany bocznej oblicz z twierdzenia Pitagorasa, gdzie szukana przekątna to przeciwprostokątna, natomiast przyprostokątne to wysokość graniastosłupa oraz krawędź podstawy. Krótszą przekątną graniastosłupa oblicz z twierdzenia Pitagorasa, gdzie przeciwprostokątna to szukana przekątna, a przyprostokątne to wysokość graniastosłupa i dwukrotność wysokości podstawy. Aby trójkąt był równoramienny dwa z trzech boków muszą być równe, dlatego musisz sprawdzić trzy konfiguracje, czyli trzy równania, wyznaczając z nich wysokość graniastosłupa.

Ćwiczenie A.
98Ćwiczenie B.
99Ćwiczenie C.
99Zadanie 3.
101Zadanie 7.
102Zadanie 8.
102Zadanie 9.
102Zadanie 10.
103Zadanie 11.
103Zadanie 18.
105Zadanie 20.
105Zadanie 21.
105Zadanie 1.
108Zadanie 2.
108Zadanie 6.
109Ćwiczenie A.
110Ćwiczenie B.
112Ćwiczenie C.
112Ćwiczenie D.
113Zadanie 1.
115Zadanie 2.
115Zadanie 6.
116Zadanie 8.
116Zadanie 9.
116Zadanie 11.
116Zadanie 12.
117Zadanie 14.
117Zadanie 1.
120Zadanie 2.
120Zadanie 3.
120Zadanie 4.
120Zadanie 6.
121Zadanie 8.
121Zadanie 9.
121Zadanie 10.
121Ćwiczenie B
124Zadanie 1.
125Zadanie 2.
125Zadanie 3
125Zadanie 7.
126Zadanie 9.
126Zadanie 14.
127Zadanie 4.
128Zadanie 6.
128Zadanie 8.
128
