Twoim zadaniem jest udowodnienie, że dla opisanej sytuacji współczynniki załamania szkła i cieczy muszą spełniać pewną określoną zależność, a mianowicie: $\text{[math]}$ .

Opis sytuacji: Masz akwarium prostopadłościenne wykonane ze szkła z określonym współczynnikiem załamania $\text{[math]}$ . Wewnątrz akwarium znajduje się ciecz z współczynnikiem załamania $\text{[math]}$ . Interesuje Cię sytuacja, w której promień światła ulega całkowitemu wewnętrznemu odbiciu.

Kiedy światło dociera do granicy ośrodka, w którym porusza się szybciej, z ośrodka, w którym porusza się wolniej (w tym przypadku ciecz), może wystąpić zjawisko całkowitego wewnętrznego odbicia przy pewnym kącie, nazywanym kątem granicznym.

Dla kąta granicznego i załamania, stosujesz prawo Snella:

$\text{[math]}$

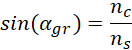
Gdzie $\text{[math]}$ to kąt graniczny.

Z własności kątów granicznych wiesz, że:

$\text{[math]}$

Co implikuje:

$\text{[math]}$

Na podstawie rysunku sytuacji oblicz:

$\text{[math]}$

Gdzie:

$\text{[math]}$

Wprowadzasz wartość zastępczą dla $\text{[math]}$ , co daje nam:

$\text{[math]}$

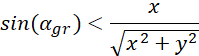
Z uwzględnieniem $\text{[math]}$ :

$\text{[math]}$

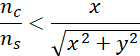
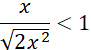
Zakładając, że $\text{[math]}$ jest mniejsze niż $\text{[math]}$ , możesz stwierdzić:

$\text{[math]}$

Skracając, otrzymujesz:

$\text{[math]}$

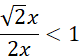
Co prowadzi do:

$\text{[math]}$

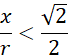
Wprowadzając wcześniejszą nierówność:

$\text{[math]}$

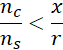
Otrzymujesz:

$\text{[math]}$

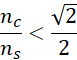
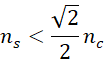
Przemnażając obie strony przez $\text{[math]}$ , dochodzisz do końcowego wyniku:

$\text{[math]}$

Całkowite wewnętrzne odbicie to zjawisko optyczne, które zachodzi, gdy światło przechodzi z ośrodka o większym współczynniku załamania do ośrodka o mniejszym współczynnikiem załamania przy kącie padania większym niż tzw. kąt graniczny.

W tym zadaniu bierzesz pod uwagę akwarium wykonane ze szkła (o współczynniku załamania $\text{[math]}$ ) i ciecz zawartą wewnątrz (o współczynnikiem załamania $\text{[math]}$ ). Światło, przechodząc przez te dwa ośrodki, ulega całkowitemu wewnętrznemu odbiciu w dwóch punktach. Aby to zjawisko mogło zachodzić, konieczne jest spełnienie pewnych warunków odnośnie stosunku współczynników załamania obu ośrodków.

Przy wykorzystaniu prawa Snella i podstawowych zasad trygonometrii możesz sformułować matematyczne warunki, które muszą być spełnione, aby promień światła uległ całkowitemu wewnętrznemu odbiciu. Twoje rozwiązanie prowadzi do wniosku, że współczynnik załamania szkła musi być mniejszy niż wartość $\text{[math]}$ razy współczynnik załamania cieczy, czyli $\text{[math]}$ .

W praktyce oznacza to, że ciecz w akwarium musi mieć stosunkowo wysoki współczynnik załamania w porównaniu do szkła, aby zaobserwować opisane w zadaniu zjawisko całkowitego wewnętrznego odbicia w obu punktach.