Dane:
- Aktywność próbki o godzinie 10:05:![]()
- - Początkowa aktywność próbki przed tą godziną: ![]()
- Czas półrozpadu izotopu jodu-128: ![]()
Wzór na aktywność próbki po pewnym czasie rozpadu jej początkowej liczby jąder promieniotwórczych:
![]()
Gdzie:
![]()
![]()
![]()
![]()
Przekształcając równanie w celu znalezienia ![]()
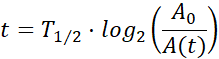
Podstawiając wartości liczbowe, otrzymujesz:
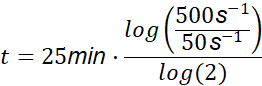
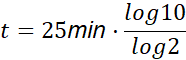
![]()
To jest równoznaczne z 1 godziną i 23 minutami.
Ostateczne obliczenia:
10:05 - 1 godzina 23 minuty = 8:42.
Odpowiedź: Próbka emitowała 500 kwantów na sekundę o godzinie 8:42.

W zadaniu masz do czynienia z obliczeniem czasu, w którym próbka jodu-128 miała początkową aktywność 500 kwantów promieniowania na sekundę. Wiesz, że aktywność próbki spadła do 50 kwantów na sekundę o godzinie 10:05 i że czas półrozpadu tego izotopu wynosi 25 minut.
Aby rozwiązać to zadanie:
1. Używasz wzoru opartego na logarytmach, który pozwala obliczyć czas na podstawie zmiany aktywności.
2. Wyrażenie to zawiera logarytm o podstawie 2, ale można je przekształcić przy pomocy logarytmu naturalnego, korzystając z właściwości logarytmów.
3. Po podstawieniu znanych wartości (aktywność początkowa i aktywność w danym momencie) do wzoru, oblicz czas.
4. Otrzymany czas \ to różnica między początkową aktywnością a momentem, w którym aktywność spadła do 50 kwantów na sekundę. Odejmując ten czas od godziny 10:05, otrzymujesz godzinę, w której próbka miała początkową aktywność 500 kwantów na sekundę.
Podsumowując, kluczem do rozwiązania tego zadania jest zrozumienie, jak zmienia się aktywność w czasie oraz umiejętność zastosowania odpowiedniego wzoru z logarytmami do obliczenia poszukiwanego czasu.