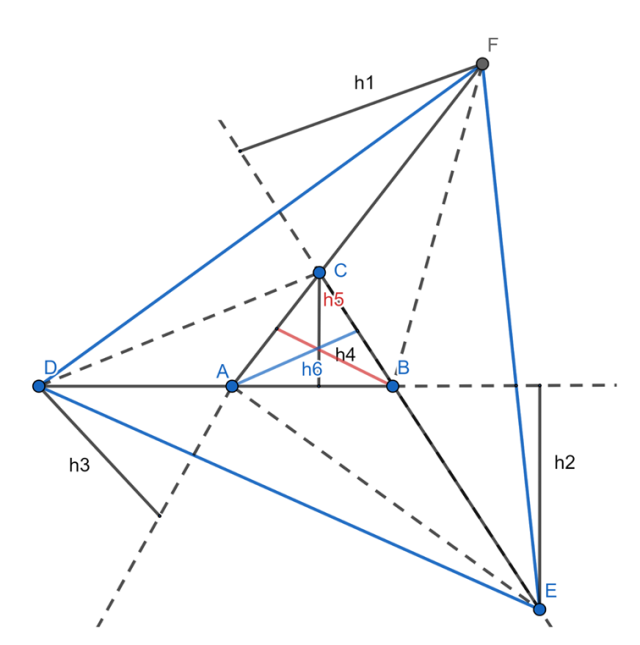
Boki trójkąta równobocznego ABC zostały przedłużone (rysunek obok) tak że długość każdego z odcinków AD, BE i CF jest równa długości boku tego trójkąta. Uzasadnij, dlaczego pole trójkąta DEF jest siedmiokrotnie większe niż pole trójkąta ABC.
![]()
AD = BE = CF = AB = BC = AC = a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|DB| = |CE| = |AF|
![]()
![]()
|DA| = |AC| = a
![]()
![]()
![]()
![]()
![]()
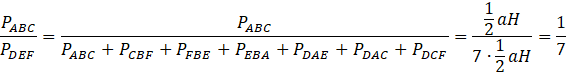

Zauważ, że możesz obliczyć pole trójkąta DEF jako sumę
![]() Wiemy, że AD = BE = CF = AB = BC = AC = a. Oblicz pole trójkąta ABC na trzy różne sposoby i zauważ, że
Wiemy, że AD = BE = CF = AB = BC = AC = a. Oblicz pole trójkąta ABC na trzy różne sposoby i zauważ, że
![]() . Zauważ, że
. Zauważ, że
![]() , ponieważ te trójkąty składają się z trzech boków identycznej długości. Pamiętając, że |DB| = |CE| = |AF| możesz wyciągnąć wniosek, że
, ponieważ te trójkąty składają się z trzech boków identycznej długości. Pamiętając, że |DB| = |CE| = |AF| możesz wyciągnąć wniosek, że
![]() . Następnie oblicz pole trójkąta DAC na dwa sposoby, aby zauważyć, że
. Następnie oblicz pole trójkąta DAC na dwa sposoby, aby zauważyć, że
![]() , czyli
, czyli
![]() . Możemy zauważyć, że pole każdego z trójkątów ABC, CBD, FBE, EBA, DAE, DAC, DCF da się obliczyć identycznym wzorem
. Możemy zauważyć, że pole każdego z trójkątów ABC, CBD, FBE, EBA, DAE, DAC, DCF da się obliczyć identycznym wzorem
![]() Oznacza to, że wszystkie te trójkąty mają takie samo pole. Na koniec oblicz stosunek
Oznacza to, że wszystkie te trójkąty mają takie samo pole. Na koniec oblicz stosunek
![]() i zauważ, że pole trójkąta ABC stanowi
i zauważ, że pole trójkąta ABC stanowi
![]() pola trójkąta DEF.
pola trójkąta DEF.

Zadanie 1.
46Zadanie 2.
46Zadanie 3.
46Zadanie 4.
46Zadanie 8.
46Zadanie 9.
47Zadanie 11.
47Zadanie 13.
47Zadanie 23.
49Zadanie 27.
49Zadanie 29.
49Zadanie 37.
50Zadanie 3.
52Zadanie 16.
54Zadanie 20.
54Zadanie 22.
54Zadanie 29.
56Zadanie 2.
58Zadanie 6.
58Zadanie 8.
59Zadanie 16.
60Zadanie 1.
61Zadanie 2.
61Zadanie 3.
61Zadanie 10.
62Zadanie 16.
62Zadanie 19.
62Zadanie 7.
64Zadanie 8.
65Zadanie 11.
65
