Wykaż, że trójkąty APS i CQS są przestające jeśli w trójkącie równobocznym ABC przedstawionym na rysunku na bokach AB i BC wybrano odpowiednio punkty P i Q tak, że
![]() i
i
![]() , a odcinki AQ i CP przecinają się w punkcie S.
, a odcinki AQ i CP przecinają się w punkcie S.
Niech
![]() – bok trójkąta ABC. Skoro jest on równoboczny, to wszystkie jego boki będą miały taką długość, więc:
– bok trójkąta ABC. Skoro jest on równoboczny, to wszystkie jego boki będą miały taką długość, więc:
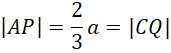
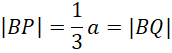
Trójkąty ABQ i CPB są przystające na podstawie cechy BKB
![]() .
.
Skoro powyższe trójkąty są przystające, to odpowiadające sobie kąty mają takie same miary, czyli:
![]() , co oznacza, że:
, co oznacza, że:
![]()
Dodatkowo:
![]() - kąty wierzchołkowe
- kąty wierzchołkowe
Skoro dwa kąty w obu trójkątach ASP i CQS są takie same, to trzeci również, więc:
![]()
Więc trójkąty APS i CQS są przystające z cechy KBK
![]() .
.
To kończy dowód.


Zadanie 1
274Ćwiczenie 1
275Ćwiczenie 2
276Zadanie 1
276Zadanie 3
277Zadanie 5
277Zadanie 10
277Ćwiczenie 2
280Ćwiczenie 3
280Ćwiczenie 5
281Ćwiczenie 6
281Zadanie 1
282Zadanie 8
282Ćwiczenie 1
283Ćwiczenie 2
283Ćwiczenie 5
284Ćwiczenie 6
284Zadanie 1
285Zadanie 5
285Zadanie 6
286Ćwiczenie 1
287Ćwiczenie 2
287Ćwiczenie 3
288Ćwiczenie 4
289Ćwiczenie 5
289Zadanie 1
289Zadanie 3
289Zadanie 5
290Zadanie 12
290Ćwiczenie 2
291Ćwiczenie 3
291Ćwiczenie 5
292Zadanie 2
292Zadanie 3
293Zadanie 4
293Zadanie 5
293Zadanie 6
293Zadanie 7
293Zadanie 11
294Zadanie 13
294Zadanie 14
294Zadanie 1
296Zadanie 2
296Zadanie 4
296Ćwiczenie 1
297Ćwiczenie 3
298Ćwiczenie 5
298Ćwiczenie 6
298Zadanie 1
299Zadanie 3
299Zadanie 5
299Zadanie 14
300Ćwiczenie 1
302Zadanie 1
303Zadanie 1
306Zadanie 3
306Zadanie 4
306Zadanie 1
307Zadanie 2
307Zadanie 5
307Zadanie 7
307
