Wykaż, że proste zawierające wysokości trójkąta przecinają się w jednym punkcie.
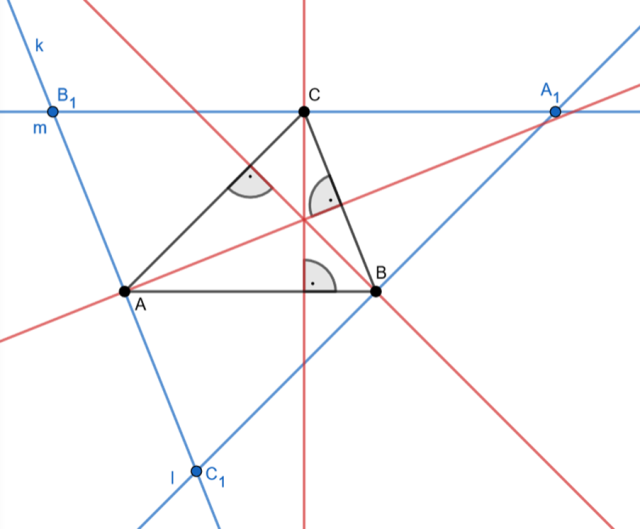
Prosta
![]() jest równoległa do boku AC, więc odcinki BA1 i AC są równoległe. Prosta
jest równoległa do boku AC, więc odcinki BA1 i AC są równoległe. Prosta
![]() jest równoległa do boku AB, więc odcinki CA1 i AB są równoległe. Oznacza to, że czworokąt ABA1C jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
jest równoległa do boku AB, więc odcinki CA1 i AB są równoległe. Oznacza to, że czworokąt ABA1C jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
![]()
Prosta
![]() jest równoległa do boku BC, więc odcinki AB1 i BC są równoległe. Prosta
jest równoległa do boku BC, więc odcinki AB1 i BC są równoległe. Prosta
![]() jest równoległa do boku AB, więc odcinki CB1 i AB są równoległe. Oznacza to, że czworokąt ABCB1 jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
jest równoległa do boku AB, więc odcinki CB1 i AB są równoległe. Oznacza to, że czworokąt ABCB1 jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
![]()
Prosta
![]() jest równoległa do boku BC, więc odcinki AC1 i BC są równoległe. Prosta
jest równoległa do boku BC, więc odcinki AC1 i BC są równoległe. Prosta
![]() jest równoległa do boku AC, więc odcinki BC1 i AC są równoległe. Oznacza to, że czworokąt ACBC1 jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
jest równoległa do boku AC, więc odcinki BC1 i AC są równoległe. Oznacza to, że czworokąt ACBC1 jest równoległobokiem, ponieważ ma dwie pary boków równoległych. Więc:
![]()
Dodatkowo z powyższych równości wynika, że
![]()
![]()
![]()
Z równości
![]() wynika, że punkty A, B i C są odpowiednio środkami boków B1C1, A1C1 oraz A1B1.
wynika, że punkty A, B i C są odpowiednio środkami boków B1C1, A1C1 oraz A1B1.
Zauważ, że skoro punkty ABC są środkami boków B1C1, A1C1, A1B1 i są prostopadłe do boków BC, AC, AB, to są ich symetralnymi, a wysokości poprowadzone z wierzchołków trójkąta ABC są symetralnymi boków, których są środkami.
Oznacza to, że wysokości trójkąta ABC zawierają się w symetralnych trójkąta A1B1C1, więc punkt przecięcia wysokości jest jednocześnie punktem przecięcia symetralnych.
To kończy dowód.


Zadanie 1
274Ćwiczenie 1
275Ćwiczenie 2
276Zadanie 1
276Zadanie 3
277Zadanie 5
277Zadanie 10
277Ćwiczenie 2
280Ćwiczenie 3
280Ćwiczenie 5
281Ćwiczenie 6
281Zadanie 1
282Zadanie 8
282Ćwiczenie 1
283Ćwiczenie 2
283Ćwiczenie 5
284Ćwiczenie 6
284Zadanie 1
285Zadanie 5
285Zadanie 6
286Ćwiczenie 1
287Ćwiczenie 2
287Ćwiczenie 3
288Ćwiczenie 4
289Ćwiczenie 5
289Zadanie 1
289Zadanie 3
289Zadanie 5
290Zadanie 12
290Ćwiczenie 2
291Ćwiczenie 3
291Ćwiczenie 5
292Zadanie 2
292Zadanie 3
293Zadanie 4
293Zadanie 5
293Zadanie 6
293Zadanie 7
293Zadanie 11
294Zadanie 13
294Zadanie 14
294Zadanie 1
296Zadanie 2
296Zadanie 4
296Ćwiczenie 1
297Ćwiczenie 3
298Ćwiczenie 5
298Ćwiczenie 6
298Zadanie 1
299Zadanie 3
299Zadanie 5
299Zadanie 14
300Ćwiczenie 1
302Zadanie 1
303Zadanie 1
306Zadanie 3
306Zadanie 4
306Zadanie 1
307Zadanie 2
307Zadanie 5
307Zadanie 7
307
