Wyznacz obwody trójkątów BDE i PQR, jeśli punkty P, Q i R są środkami odcinków: AB, BC i DE oraz
![]() i
i
![]() .
.
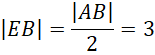
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
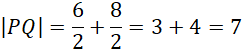
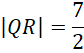
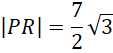
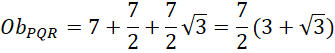

Zauważ, że trójkąt o kątach
![]() jest szczególny. Długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
jest szczególny. Długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
![]() razy dłuższa od długości boku naprzeciwko najmniejszego kąta. Na tej podstawie wyznacz długość boku EB w trójkącie ABE oraz boku BD w trójkącie BCD.
razy dłuższa od długości boku naprzeciwko najmniejszego kąta. Na tej podstawie wyznacz długość boku EB w trójkącie ABE oraz boku BD w trójkącie BCD.
Następnie oblicz miarę kąta ABD korzystając z tego, że suma miar kątów ABE, EBD i CBD wynosi
![]() , ponieważ są to kąty przyległe i na tej podstawie oblicz miarę środkowego z nich.
, ponieważ są to kąty przyległe i na tej podstawie oblicz miarę środkowego z nich.
Zauważ, że skoro trójkąt BDE jest prostokątny możesz skorzystać z twierdzenia Pitagorasa i obliczyć długość przeciwprostokątnej, a następnie jego obwód.
Na koniec ponownie skorzystaj z tego, że trójkąt PQR ma kąty o mierze
![]() i jest szczególny. Na tej podstawie oblicz jego obwód.
i jest szczególny. Na tej podstawie oblicz jego obwód.

Zadanie 1
274Ćwiczenie 1
275Ćwiczenie 2
276Zadanie 1
276Zadanie 3
277Zadanie 5
277Zadanie 10
277Ćwiczenie 2
280Ćwiczenie 3
280Ćwiczenie 5
281Ćwiczenie 6
281Zadanie 1
282Zadanie 8
282Ćwiczenie 1
283Ćwiczenie 2
283Ćwiczenie 5
284Ćwiczenie 6
284Zadanie 1
285Zadanie 5
285Zadanie 6
286Ćwiczenie 1
287Ćwiczenie 2
287Ćwiczenie 3
288Ćwiczenie 4
289Ćwiczenie 5
289Zadanie 1
289Zadanie 3
289Zadanie 5
290Zadanie 12
290Ćwiczenie 2
291Ćwiczenie 3
291Ćwiczenie 5
292Zadanie 2
292Zadanie 3
293Zadanie 4
293Zadanie 5
293Zadanie 6
293Zadanie 7
293Zadanie 11
294Zadanie 13
294Zadanie 14
294Zadanie 1
296Zadanie 2
296Zadanie 4
296Ćwiczenie 1
297Ćwiczenie 3
298Ćwiczenie 5
298Ćwiczenie 6
298Zadanie 1
299Zadanie 3
299Zadanie 5
299Zadanie 14
300Ćwiczenie 1
302Zadanie 1
303Zadanie 1
306Zadanie 3
306Zadanie 4
306Zadanie 1
307Zadanie 2
307Zadanie 5
307Zadanie 7
307
