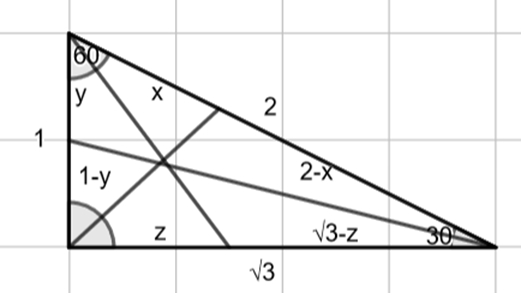
Oblicz długości odcinków na jakie dwusieczne kątów trójkąta o kątach
![]() dzielą jego boki, jeśli jego przeciwprostokątna ma długość 2
dzielą jego boki, jeśli jego przeciwprostokątna ma długość 2
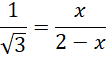
![]()
![]()
![]()
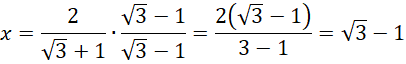
![]()
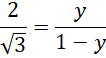
![]()
![]()
![]()
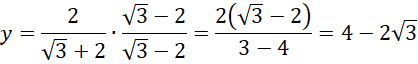
![]()
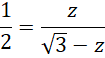
![]()
![]()
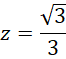
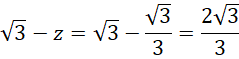

Zauważ, że trójkąt o kątach
![]() jest szczególny. Długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
jest szczególny. Długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najkrótszego kąta, a długość boku naprzeciwko średniego kąta jest
![]() razy dłuższa od długości boku naprzeciwko najmniejszego kąta.
razy dłuższa od długości boku naprzeciwko najmniejszego kąta.
Zauważ, że w tym przypadku przeciwprostokątna ma długość 2 i znajduję się ona naprzeciwko największego kąta, więc długość boku naprzeciwko najkrótszego kąta jest dwa razy krótsza, czyli ma długość 1, zaś długość boku naprzeciwko średniego kąta wynosi
![]()
Zacznij od dwusiecznej kąta prostego. Skorzystaj z tego, że dwusieczna kąta w trójkącie dzieli przeciwległy bok na odcinki proporcjonalne do pozostałych boków trójkąta. Zapisz to za pomocą równania i wyznacz z niego wartość
![]() Pamiętaj o usunięciu niewymierności z mianownika, czyli pomnożeniu licznika i mianownika ułamka przez wartość mianownika z przeciwnym znakiem pomiędzy wyrażeniami.
Pamiętaj o usunięciu niewymierności z mianownika, czyli pomnożeniu licznika i mianownika ułamka przez wartość mianownika z przeciwnym znakiem pomiędzy wyrażeniami.
Następnie w podobny sposób oblicz długości powstałych odcinków dla dwusiecznej kąta
![]() oraz dla dwusiecznej kąta
oraz dla dwusiecznej kąta
![]() .
.

Zadanie 1
274Ćwiczenie 1
275Ćwiczenie 2
276Zadanie 1
276Zadanie 3
277Zadanie 5
277Zadanie 10
277Ćwiczenie 2
280Ćwiczenie 3
280Ćwiczenie 5
281Ćwiczenie 6
281Zadanie 1
282Zadanie 8
282Ćwiczenie 1
283Ćwiczenie 2
283Ćwiczenie 5
284Ćwiczenie 6
284Zadanie 1
285Zadanie 5
285Zadanie 6
286Ćwiczenie 1
287Ćwiczenie 2
287Ćwiczenie 3
288Ćwiczenie 4
289Ćwiczenie 5
289Zadanie 1
289Zadanie 3
289Zadanie 5
290Zadanie 12
290Ćwiczenie 2
291Ćwiczenie 3
291Ćwiczenie 5
292Zadanie 2
292Zadanie 3
293Zadanie 4
293Zadanie 5
293Zadanie 6
293Zadanie 7
293Zadanie 11
294Zadanie 13
294Zadanie 14
294Zadanie 1
296Zadanie 2
296Zadanie 4
296Ćwiczenie 1
297Ćwiczenie 3
298Ćwiczenie 5
298Ćwiczenie 6
298Zadanie 1
299Zadanie 3
299Zadanie 5
299Zadanie 14
300Ćwiczenie 1
302Zadanie 1
303Zadanie 1
306Zadanie 3
306Zadanie 4
306Zadanie 1
307Zadanie 2
307Zadanie 5
307Zadanie 7
307
