Wykaż, że trójkąty A’D’P i BDP są przystające, a A’D’C i ADC są podobne oraz uzasadnij prawdziwość proporcji
![]() korzystając z równości
korzystając z równości
![]() , jeśli w trójkącie ABC poprowadzono dwusieczną CD kąta
, jeśli w trójkącie ABC poprowadzono dwusieczną CD kąta
![]() , punkt A’ leży na prostej CA, odcinek A’B jest prostopadły do dwusiecznej CD i przecina ją w punkcie P, a odcinek A’D’ jest równoległy do odcinka AD.
, punkt A’ leży na prostej CA, odcinek A’B jest prostopadły do dwusiecznej CD i przecina ją w punkcie P, a odcinek A’D’ jest równoległy do odcinka AD.
Na podstawie treści zadania i rysunku wiesz, że:
![]()
Zauważ że:
![]() - kąty wierzchołkowe
- kąty wierzchołkowe
![]() oraz
oraz
![]() – kąty naprzemianległe, ponieważ proste
– kąty naprzemianległe, ponieważ proste
![]() oraz
oraz
![]() są równoległe
są równoległe
Dodatkowo
![]() , więc trójkąty A’PD’ i BPD są przystające z cechy KBK.
, więc trójkąty A’PD’ i BPD są przystające z cechy KBK.
Zauważ że:
![]()
![]() oraz
oraz
![]() – kąty odpowiadające, ponieważ proste
– kąty odpowiadające, ponieważ proste
![]() oraz
oraz
![]() są równoległe
są równoległe
Więc trójkąty A’D’C i ADC są przystające z cechy KKK.
Więc:
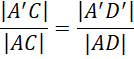
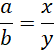
To kończy dowód.


Zadanie 1
274Ćwiczenie 1
275Ćwiczenie 2
276Zadanie 1
276Zadanie 3
277Zadanie 5
277Zadanie 10
277Ćwiczenie 2
280Ćwiczenie 3
280Ćwiczenie 5
281Ćwiczenie 6
281Zadanie 1
282Zadanie 8
282Ćwiczenie 1
283Ćwiczenie 2
283Ćwiczenie 5
284Ćwiczenie 6
284Zadanie 1
285Zadanie 5
285Zadanie 6
286Ćwiczenie 1
287Ćwiczenie 2
287Ćwiczenie 3
288Ćwiczenie 4
289Ćwiczenie 5
289Zadanie 1
289Zadanie 3
289Zadanie 5
290Zadanie 12
290Ćwiczenie 2
291Ćwiczenie 3
291Ćwiczenie 5
292Zadanie 2
292Zadanie 3
293Zadanie 4
293Zadanie 5
293Zadanie 6
293Zadanie 7
293Zadanie 11
294Zadanie 13
294Zadanie 14
294Zadanie 1
296Zadanie 2
296Zadanie 4
296Ćwiczenie 1
297Ćwiczenie 3
298Ćwiczenie 5
298Ćwiczenie 6
298Zadanie 1
299Zadanie 3
299Zadanie 5
299Zadanie 14
300Ćwiczenie 1
302Zadanie 1
303Zadanie 1
306Zadanie 3
306Zadanie 4
306Zadanie 1
307Zadanie 2
307Zadanie 5
307Zadanie 7
307
