W tym zadaniu podaj, ile wynosi odległość środka okręgu opisanego na trójkącie
![]() o wierzchołkach
o wierzchołkach
![]() od środka ciężkości tego trójkąta.
od środka ciężkości tego trójkąta.
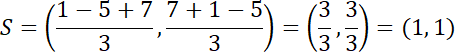
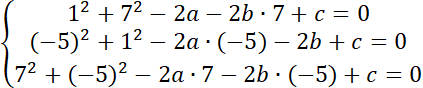
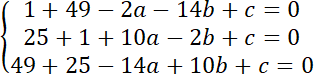
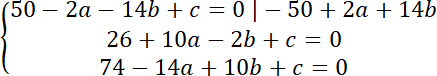
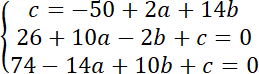
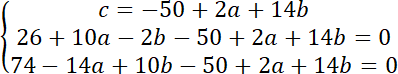
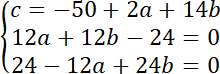
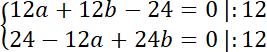
![]()
![]()
![]()
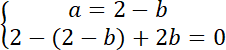
![]()
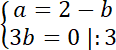
![]()
![]()
![]()
![]()
Odpowiedź: Odległość wynosi
![]() .
.

Oblicz środek ciężkości trójkąta ze wzoru:
![]()
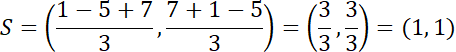
Środek okręgu opisanego na trójkącie znajduje się w takiej samej odległości od wszystkich trzech wierzchołków, ponieważ leżą one na okręgu. Możesz zapisać to w formie układu równań:
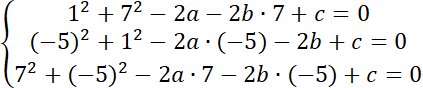
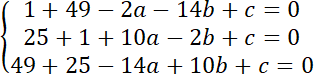
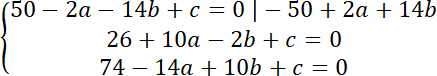
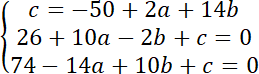
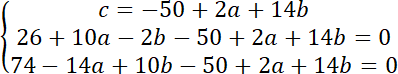
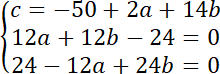
Aby znaleźć środek okręgu rozwiąż układ równań:
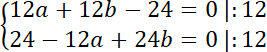
![]()
![]()
![]()
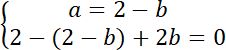
![]()
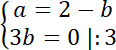
![]()
![]()
Stąd środek okręgu to
![]() . Oblicz odległość środka okręgu od środka ciężkości:
. Oblicz odległość środka okręgu od środka ciężkości:
![]()

Zadanie 1.5
111Zadanie 1.6
111Zadanie 1.7
111Zadanie 1.8
111Zadanie 1.9
111Zadanie 1.10
111Zadanie 1.11
112Zadanie 1.12
112Zadanie 1.13
112Zadanie 1.14
112Zadanie 1.18
112Zadanie 1.19
112Zadanie 1.20
113Zadanie 1.21
113Zadanie 1.22
113Zadanie 1.23
113Zadanie 1.26
113Zadanie 2.4
121Zadanie 2.5
121Zadanie 2.6
121Zadanie 2.7
122Zadanie 2.8
122Zadanie 2.9
122Zadanie 2.10
122Zadanie 2.11
122Zadanie 2.14
122Zadanie 2.16
123Zadanie 3.4
134Zadanie 3.5
134Zadanie 3.6
134Zadanie 3.7
134Zadanie 3.8
134Zadanie 3.10
134Zadanie 3.15
135Zadanie 3.17
135Zadanie 3.19
135Zadanie 3.20
135Zadanie 3.25
136Zadanie 4.4
144Zadanie 4.5
144Zadanie 4.6
144Zadanie 4.7
144Zadanie 4.9
145Zadanie 4.10
145Zadanie 4.11
145Zadanie 4.12
145Zadanie 4.15
145Zadanie 4.19
145Zadanie 4.22
146Zadanie 5.5
156Zadanie 5.6
156Zadanie 5.7
157Zadanie 5.14
157Zadanie 5.25
158Zadanie 5.26
158Zadanie 5.27
158Zadanie 5.29
159Zadanie 5.30
159Zadanie 6.6
168Zadanie 6.7
168Zadanie 6.10
168Zadanie 6.11
168Zadanie 6.14
169Zadanie 6.17
169Zadanie 6.18
169Zadanie 6.19
169Zadanie 6.22.
170Zadanie 6.23.
170Zadanie 7.4.
176Zadanie 7.5.
176Zadanie 7.6.
176Zadanie 7.8.
176Zadanie 7.9.
177Zadanie 7.11.
177Zadanie 7.13.
178Zadanie 7.14.
178Zadanie 7.15.
178Zadanie 7.18.
178Zadanie 7.19.
179Zadanie 39.
184Zadanie 40.
184Zadanie 41.
185Zadanie 42.
185Zadanie 43.
185Zadanie 44.
185Zadanie 54.
186Zadanie 68.
187Zadanie 73.
188
