W tym zadaniu wskaż zbiór punktów płaszczyzny kartezjańskiej, który jest opisany za pomocą układu warunków
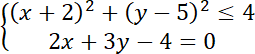 .
.
![]()
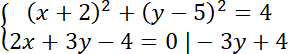
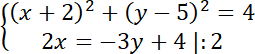
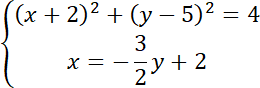
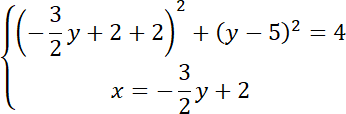
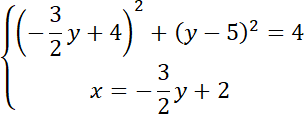
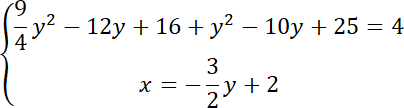
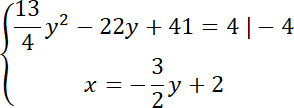
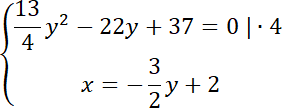
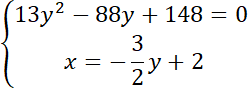
![]()
![]()
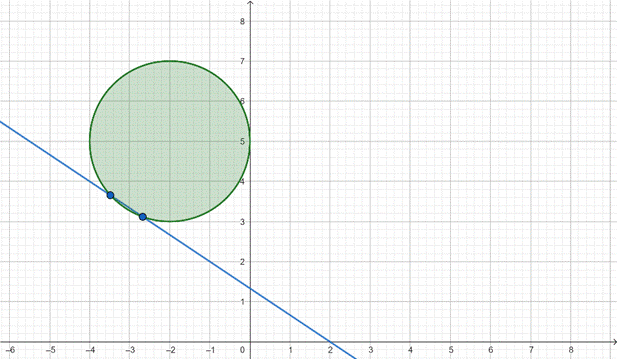
Odpowiedź: Zbiór punktów, będzie odcinkiem.
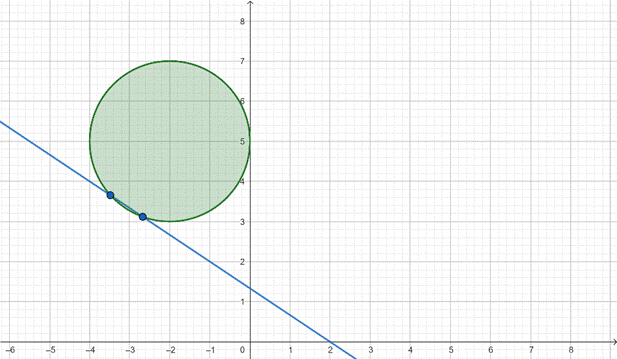

Pierwsza nierówność to koło o środku i promieniu:
![]()
Drugie to równanie prostej.
Policz przecięcie się obu figur. Zapisz układ równań dla prostej i okręgu:
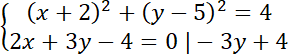
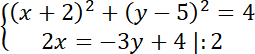
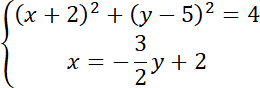
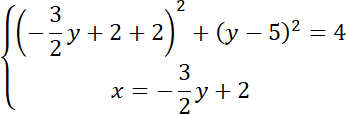
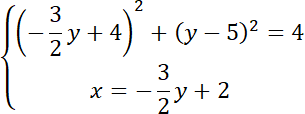
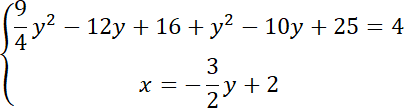
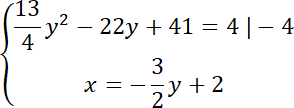
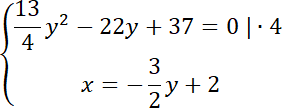
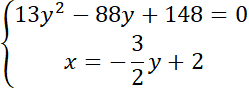
Rozwiąż równanie kwadratowe:
![]()
![]()
Zatem wiesz, że będą dwa różne rozwiązania dla y. Oznacza to, że są dwa punkty przecięcia. Stąd zbiór punktów, który jest częścią wspólną koła i kawałka prostej będzie odcinkiem.

Zadanie 1.5
111Zadanie 1.6
111Zadanie 1.7
111Zadanie 1.8
111Zadanie 1.9
111Zadanie 1.10
111Zadanie 1.11
112Zadanie 1.12
112Zadanie 1.13
112Zadanie 1.14
112Zadanie 1.18
112Zadanie 1.19
112Zadanie 1.20
113Zadanie 1.21
113Zadanie 1.22
113Zadanie 1.23
113Zadanie 1.26
113Zadanie 2.4
121Zadanie 2.5
121Zadanie 2.6
121Zadanie 2.7
122Zadanie 2.8
122Zadanie 2.9
122Zadanie 2.10
122Zadanie 2.11
122Zadanie 2.14
122Zadanie 2.16
123Zadanie 3.4
134Zadanie 3.5
134Zadanie 3.6
134Zadanie 3.7
134Zadanie 3.8
134Zadanie 3.10
134Zadanie 3.15
135Zadanie 3.17
135Zadanie 3.19
135Zadanie 3.20
135Zadanie 3.25
136Zadanie 4.4
144Zadanie 4.5
144Zadanie 4.6
144Zadanie 4.7
144Zadanie 4.9
145Zadanie 4.10
145Zadanie 4.11
145Zadanie 4.12
145Zadanie 4.15
145Zadanie 4.19
145Zadanie 4.22
146Zadanie 5.5
156Zadanie 5.6
156Zadanie 5.7
157Zadanie 5.14
157Zadanie 5.25
158Zadanie 5.26
158Zadanie 5.27
158Zadanie 5.29
159Zadanie 5.30
159Zadanie 6.6
168Zadanie 6.7
168Zadanie 6.10
168Zadanie 6.11
168Zadanie 6.14
169Zadanie 6.17
169Zadanie 6.18
169Zadanie 6.19
169Zadanie 6.22.
170Zadanie 6.23.
170Zadanie 7.4.
176Zadanie 7.5.
176Zadanie 7.6.
176Zadanie 7.8.
176Zadanie 7.9.
177Zadanie 7.11.
177Zadanie 7.13.
178Zadanie 7.14.
178Zadanie 7.15.
178Zadanie 7.18.
178Zadanie 7.19.
179Zadanie 39.
184Zadanie 40.
184Zadanie 41.
185Zadanie 42.
185Zadanie 43.
185Zadanie 44.
185Zadanie 54.
186Zadanie 68.
187Zadanie 73.
188
