Oblicz iloraz prędkości dźwięku w parze wodnej i dwutlenku węgla w tej samej temperaturze, wiedząc, że ich współczynniki adiabaty są takie same i mają wartość κ = 1,33.
Dane:
κ = 1,33
Skorzystajmy ze wzoru:
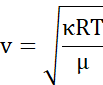
Więc:
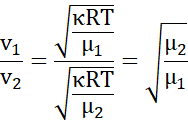
Masy molowe:
pary wodnej: ![]()
dwutlenku węgla: ![]()
Więc:
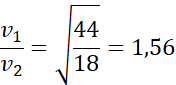
Odpowiedź: Dźwięk rozchodzi się w parze wodnej około 1,56 razy szybciej niż w dwutlenku węgla.

Skorzystaj ze wzoru na prędkość dźwięku w gazach (pierwiastek z iloczynu współczynnika adiabaty, stałej gazowej i temperatury, podzielonego przez masę molową gazu). Zauważ, podczas dzielenia pierwiastków skrócą się współczynnik adiabaty, stała gazowa oraz temperatura. Masy molowe podanych gazów odczytaj z tabel.

Zadanie 10.1.2.
191Zadanie 10.1.3.
191Zadanie 10.3.8.
203Zadanie 10.3.13.
203Zadanie 10.2.1.
195Zadanie 10.2.4.
196Zadanie 10.2.5.
196Zadanie 10.2.6.
196Zadanie 10.2.12.
197Zadanie 10.4.2.
208Zadanie 10.4.8.
208Zadanie 10.4.9.
209Zadanie 10.4.12.
209Zadanie 10.4.14.
209Zadanie 10.5.1.
213Zadanie 10.5.2.
213Zadanie 10.5.7.
214Zadanie 10.5.14.
216Zadanie 10.5.17.
217Zadanie 10.6.3.
225Zadanie 10.6.4.
225Zadanie 10.6.10.
226Zadanie 10.6.14.
227Zadanie 10.6.15.
227Zadanie 10.7.3.
240Zadanie 10.7.4.
241Zadanie 10.7.5.
241Zadanie 10.7.6.
241Zadanie 10.7.11.
242Zadanie 10.7.12.
242Zadanie 10.7.16.
243Zadanie 10.7.18.
243Zadanie 10.7.19.
243Zadanie 10.7.21.
244Zadanie 10.8.2.
249Zadanie 10.8.3.
249Zadanie 10.8.8.
250Zadanie 10.8.9.
250Zadanie 10.8.12.
251Zadanie 10.6.
252Zadanie 1. Piszczałki organowe
257Zadanie 2. Karetka pogotowia
275Zadanie 3. Rozchodzenie się dźwięku
259Zadanie 4. Rogi przeciwmgielne
259Zadanie 5. Pomiar prędkości dźwięku
260Zadanie 6. Klamerki
261
