Należy rozwiązać równanie |x + 2| = –1. Trzeba zastanowić się, czy można je rozwiązać, wykorzystując metodę (twierdzenie 1), czy skorzystać z wykresu odpowiedniej funkcji.
równanie |x + 2| = –1, nie ma rozwiązania dla x ⋲R
Sprawdźmy to równanie, korzystając z wykresu funkcji |x + 2|
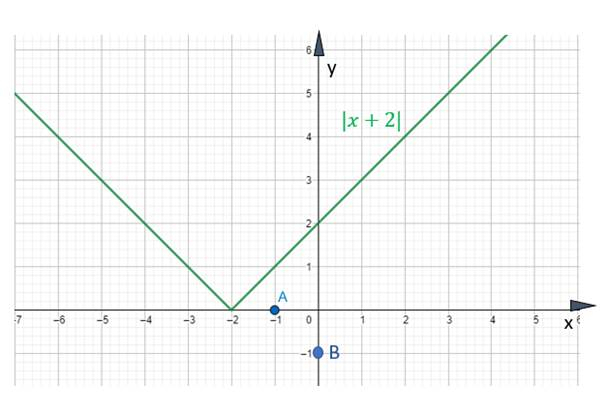

Wyrażenie |x + 2| = –1 jest sprzeczne, ponieważ wyrażenie wyciągnięte spod wartości bezwzględnej jest zawsze większe bądź równe 0.
Po narysowaniu wykresu funkcji |x + 2| widać, że zarówno x = –1 [punkt A(–1,0)], jak i y = –1 [punkt B(0,–1)] nie znajduje się na wykresie funkcji, co dowodzi, że równanie jest sprzeczne.

Zadanie 1.
42Zadanie 2.
42Zadanie 3.
42Zadanie 4.
43Zadanie 5.
43Zadanie 6.
43Zadanie 7.
43Zadanie 8.
43Zadanie 9.
43Zadanie 1.
45Zadanie 2.
44Zadanie 3.
45Zadanie 1.
48Zadanie 2.
48Zadanie 3.
48Zadanie 4.
48Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Ćwiczenie 1.
49Ćwiczenie 2.
49Ćwiczenie 3.
51Zadanie 1.
52Zadanie 2.
52Zadanie 3.
52Zadanie 4.
52Zadanie 5.
53Zadanie 6.
53Zadanie 7.
53Zadanie 8.
53Zadanie 9.
53Zadanie 10.
53Zadanie 11.
53Zadanie 12.
53Zadanie 13.
53Zadanie 15.
55Zadanie 17.
53Zadanie 23.
55
