W tym zadaniu należy rozwiązać równanie, czyli wyznaczyć wartość liczby x.
2(3–|x + 2|) = 5|–2–x| + 8–4|2 + x|
2(3–|x + 2|) = 5|(–)[2 + x]| + 8–4|2 + x|
2(3–|x + 2|) = 5|2 + x| + 8–4|2 + x|
2(3–|x + 2|) = |2 + x| + 8
6–2|x + 2| = |2 + x| + 8 /–|x + 2|
6–3|x + 2| = 8 /–6
–3|x + 2| = 2 /(–3)
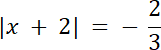
Równanie jest sprzeczne.

Najpierw należy uprościć wyrażenia wspólne, czyli po jednej stronie równania zapisać wyrażenia w wartości bezwzględnej, a po drugiej stronie pozostałą część. Następnie należy zauważyć, że wyciągnięcie znaku „–” z wartości bezwzględnej, nie spowoduje zmiany znaku tego wyrażenia, minus zostaje zredukowany, dzięki czemu zauważ, że w równaniu są takie same wyrażenia w wartości bezwzględnej. Wykonujemy kolejny raz grupowanie wyrażeń wspólnych. Wynik wyrażenia jest mniejszy od zera, a jak wiemy z definicji, wartość wyrażenia bezwzględnego jest zawsze większa bądź równa zeru, więc równanie jest sprzeczne.

Zadanie 1.
42Zadanie 2.
42Zadanie 3.
42Zadanie 4.
43Zadanie 5.
43Zadanie 6.
43Zadanie 7.
43Zadanie 8.
43Zadanie 9.
43Zadanie 1.
45Zadanie 2.
44Zadanie 3.
45Zadanie 1.
48Zadanie 2.
48Zadanie 3.
48Zadanie 4.
48Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Ćwiczenie 1.
49Ćwiczenie 2.
49Ćwiczenie 3.
51Zadanie 1.
52Zadanie 2.
52Zadanie 3.
52Zadanie 4.
52Zadanie 5.
53Zadanie 6.
53Zadanie 7.
53Zadanie 8.
53Zadanie 9.
53Zadanie 10.
53Zadanie 11.
53Zadanie 12.
53Zadanie 13.
53Zadanie 15.
55Zadanie 17.
53Zadanie 23.
55
