W tym zadaniu należy rozwiązać nierówność z wartością bezwzględną.
5|x +
![]() |–4|
|–4|
![]() + x| ≥ 3|–x–2
+ x| ≥ 3|–x–2
![]() |
|
(2
![]() )
)
5|x +
![]() |–4|
|–4|
![]() + x| ≥ 3|(–)[x + 2
+ x| ≥ 3|(–)[x + 2
![]() ]|
]|
5|x +
![]() |–4|x +
|–4|x +
![]() | ≥ 3|x +
| ≥ 3|x +
![]() | |–3|x +
| |–3|x +
![]() |
|
5|x +
![]() |–4|x +
|–4|x +
![]() |–3|x +
|–3|x +
![]() | ≥ 0
| ≥ 0
–2|x +
![]() | ≥ 0 | /(–2)
| ≥ 0 | /(–2)
|x +
![]() | ≤ 0 ⇔x +
| ≤ 0 ⇔x +
![]() = 0
= 0
x +
![]() = 0 |–
= 0 |–
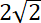
x = –
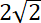
x ⋲ {–
![]() }
}

Rozwiąż nierówność z wartością bezwzględną i zauważmy, że wyrażenia:
2
![]() i |x +
i |x +
![]() | = |–x–2
| = |–x–2
![]() | są równe, więc zapisz je w jednej formie, a następnie redukujemy wspólne wyrażenia. Dochodzimy do zapisu, w którym wyrażenie w wartości bezwzględnej jest mniejsze od zera bądź równe zeru, a wiemy, że wyrażenie w wartości bezwzględnej nie może być mniejsze niż zero, więc ostatecznie zapisz i rozwiąż następujące równanie: x +
| są równe, więc zapisz je w jednej formie, a następnie redukujemy wspólne wyrażenia. Dochodzimy do zapisu, w którym wyrażenie w wartości bezwzględnej jest mniejsze od zera bądź równe zeru, a wiemy, że wyrażenie w wartości bezwzględnej nie może być mniejsze niż zero, więc ostatecznie zapisz i rozwiąż następujące równanie: x +
![]() = 0.
= 0.

Zadanie 1.
42Zadanie 2.
42Zadanie 3.
42Zadanie 4.
43Zadanie 5.
43Zadanie 6.
43Zadanie 7.
43Zadanie 8.
43Zadanie 9.
43Zadanie 1.
45Zadanie 2.
44Zadanie 3.
45Zadanie 1.
48Zadanie 2.
48Zadanie 3.
48Zadanie 4.
48Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Ćwiczenie 1.
49Ćwiczenie 2.
49Ćwiczenie 3.
51Zadanie 1.
52Zadanie 2.
52Zadanie 3.
52Zadanie 4.
52Zadanie 5.
53Zadanie 6.
53Zadanie 7.
53Zadanie 8.
53Zadanie 9.
53Zadanie 10.
53Zadanie 11.
53Zadanie 12.
53Zadanie 13.
53Zadanie 15.
55Zadanie 17.
53Zadanie 23.
55
