W tym zadaniu, na podstawie podanego zbioru rozwiązań nierówności, należy wyznaczyć nierówność.
x ⋲ (–6, 4)
x < 4 ∧ x >–6
|x–a| < b, a–punkt równoodległy; b–odległość punktów od środka punktu równoodległego x1 = –6 i x2 = 4
x2–b = b–x1
2b = x2–x1
2b = 4–(–6)
2b = 10
b = 5 , czyli:
![]()
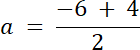
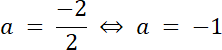
|x–a| < b
|x–(–1)| < 5
|x + 1| < 5
Odpowiedź A. |x + 1| < 5

Na podstawie zbioru rozwiązań nierówności, wybieramy skrajne punkty zbioru, szukamy punkty równoodległego od nich, a także odległości skrajnego punktu od punktu równoodległego i zapisz nierówność.

Zadanie 1.
42Zadanie 2.
42Zadanie 3.
42Zadanie 4.
43Zadanie 5.
43Zadanie 6.
43Zadanie 7.
43Zadanie 8.
43Zadanie 9.
43Zadanie 1.
45Zadanie 2.
44Zadanie 3.
45Zadanie 1.
48Zadanie 2.
48Zadanie 3.
48Zadanie 4.
48Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Ćwiczenie 1.
49Ćwiczenie 2.
49Ćwiczenie 3.
51Zadanie 1.
52Zadanie 2.
52Zadanie 3.
52Zadanie 4.
52Zadanie 5.
53Zadanie 6.
53Zadanie 7.
53Zadanie 8.
53Zadanie 9.
53Zadanie 10.
53Zadanie 11.
53Zadanie 12.
53Zadanie 13.
53Zadanie 15.
55Zadanie 17.
53Zadanie 23.
55
