Należy rozwiązać równanie 12–2|x–4| = |–x + 4|–6 zaznaczając odpowiednie punkty na osi liczbowej.
12–2|x–4| = |–x + 4|–6
12–2|x–4| = |–(x–4)|–6
12–2|x–4| = |x–4|–6
–2|x–4|–|x–4| = –6–12
–3|x–4| = –18 |/(–3)
|x–4| = 6
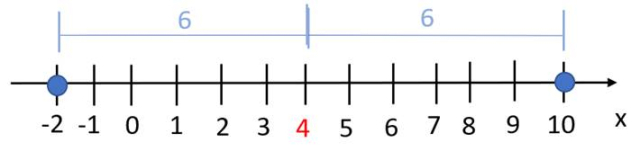

Równanie 12–2|x–4| = |–x + 4|–6 należy zapisać w uproszczonej postaci. W tym celu rozwiąż równanie, aby po lewej stronie otrzymać wyrażenie w wartości bezwzględnej, a po prawej stronie równania, do jakiej liczby zostało przyrównane. Po uproszczeniu otrzymasz zapis: |x–4| = 6. Wyrażenie |x–4| oznacza odległość szukanej liczby x od liczby 4. Zaznaczamy liczbę 4 na osi liczbowej i szukamy wszystkich liczb x, których odległość od liczby 4 jest równa 6. Szukane liczby to–2 i 10 (sprawdź, podstawiając je do równania w miejsce x). Zatem: |x–4| = 6 ⇔ (x = –2 v x = 10), czyli x ⋲ {–2, 10}.

Zadanie 1.
42Zadanie 2.
42Zadanie 3.
42Zadanie 4.
43Zadanie 5.
43Zadanie 6.
43Zadanie 7.
43Zadanie 8.
43Zadanie 9.
43Zadanie 1.
45Zadanie 2.
44Zadanie 3.
45Zadanie 1.
48Zadanie 2.
48Zadanie 3.
48Zadanie 4.
48Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Ćwiczenie 1.
49Ćwiczenie 2.
49Ćwiczenie 3.
51Zadanie 1.
52Zadanie 2.
52Zadanie 3.
52Zadanie 4.
52Zadanie 5.
53Zadanie 6.
53Zadanie 7.
53Zadanie 8.
53Zadanie 9.
53Zadanie 10.
53Zadanie 11.
53Zadanie 12.
53Zadanie 13.
53Zadanie 15.
55Zadanie 17.
53Zadanie 23.
55
