Dana jest funkcja:
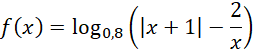
Podaj zbiór argumentów, dla których jest ona określona.
Mianownik ułamka nie może być zerem, zatem:
![]() .
.
Z definicji logarytmu wynika, że liczba logarytmowana musi być większa od 0, zatem:
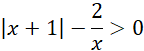
Uwzględnij dwa przypadki:
![]() gdy x > 0, lub:
gdy x > 0, lub:
![]() gdy x < 0
gdy x < 0
Wartość x = 0 została wcześniej odrzucona z dziedziny, nie jest więc uwzględniana przy powyższych nierównościach.
Rozwiąż te dwie nierówności, uwzględniając przedział wartości x. Na koniec wyznacz sumę rozwiązań obu z nich.
Rozwiąż pierwszą nierówność:
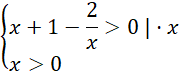
![]()
![]()
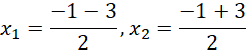
![]()
![]()
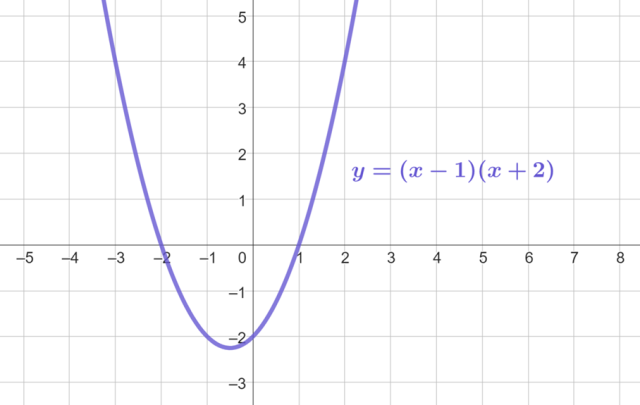
![]()
Rozwiązaniem pierwszej nierówności jest zatem:
![]()
Przejdź do drugiej nierówności:
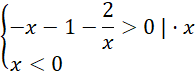
![]()
![]()
![]()
Funkcja
![]() nie ma miejsc zerowych. Jednak na podstawie faktu, że ramiona jej wykresu są skierowane w górę można określić, że leży on w całości powyżej osi x:
nie ma miejsc zerowych. Jednak na podstawie faktu, że ramiona jej wykresu są skierowane w górę można określić, że leży on w całości powyżej osi x:
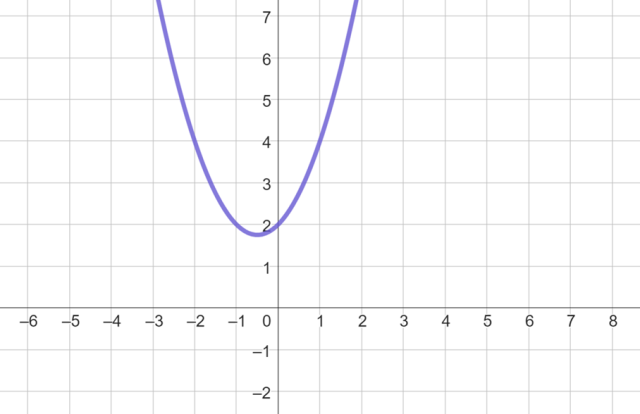
Nierówność
![]() jest zatem spełniona dla wszystkich liczb rzeczywistych.
jest zatem spełniona dla wszystkich liczb rzeczywistych.
Pozostaje tylko uwzględnić wstępny warunek, że
![]() i otrzymujemy rozwiązanie drugiej nierówności:
i otrzymujemy rozwiązanie drugiej nierówności:
![]()
Końcowym rozwiązaniem jest suma rozwiązań dwóch powyższych nierówności:
![]()
![]()
![]()

Z definicji logarytmu wynika, że liczba logarytmowana musi być większa od 0. Na podstawie tej informacji ułóż odpowiednią nierówność z wartością bezwzględną.
Rozbij nierówność na dwa przypadki w zależności od znaku liczby x.
Rozwiąż powstałe dwie nierówności, odpowiednio zdejmując wartość bezwzględną i uwzględniając przedział wartości x.
Suma ich rozwiązań jest rozwiązaniem pierwotnej nierówności i tym samym dziedziną rozpatrywanej funkcji.

Zadanie 2.1.
29Zadanie 2.2.
29Zadanie 2.3.
29Zadanie 2.4.
29Zadanie 2.5.
29Zadanie 2.6.
30Zadanie 2.7.
30Zadanie 2.8.
30Zadanie 2.9.
30Zadanie 2.10.
30Zadanie 2.11.
31Zadanie 2.19.
31Zadanie 2.25.
32Zadanie 2.26.
32Zadanie 2.28.
33Zadanie 2.29.
33Zadanie 2.30.
33Zadanie 2.31.
33Zadanie 2.32.
33Zadanie 2.33.
33Zadanie 2.34.
34Zadanie 2.35.
34Zadanie 2.36.
34Zadanie 2.37.
34Zadanie 2.38.
34Zadanie 2.40.
34Zadanie 2.41.
35Zadanie 2.42.
35Zadanie 2.43.
35Zadanie 2.44.
35Zadanie 2.45.
35Zadanie 2.46.
36Zadanie 2.47.
36Zadanie 2.48.
36Zadanie 2.49.
36Zadanie 2.52.
36Zadanie 2.53.
37Zadanie 2.54.
37Zadanie 2.55.
37Zadanie 2.56.
37Zadanie 2.57.
37Zadanie 2.58.
37Zadanie 2.59.
38Zadanie 2.60.
38Zadanie 2.61.
38Zadanie 2.62.
38Zadanie 2.63.
38Zadanie 2.64.
38Zadanie 2.65.
39Zadanie 2.66.
39Zadanie 2.67.
39Zadanie 2.68.
39Zadanie 2.69.
39Zadanie 2.70.
39Zadanie 2.71.
40Zadanie 2.72.
40Zadanie 2.73.
40Zadanie 2.74.
40Zadanie 2.75.
40Zadanie 2.76.
40Zadanie 2.77.
41Zadanie 2.78.
41Zadanie 2.79.
41Zadanie 2.80.
41Zadanie 2.81.
41Zadanie 2.82.
42Zadanie 2.83.
42Zadanie 2.84.
42Zadanie 2.85.
42Zadanie 2.86.
42Zadanie 2.87.
43Zadanie 2.90.
43Zadanie 2.91.
43Zadanie 2.92.
44Zadanie 2.93.
44Zadanie 2.94.
44Zadanie 2.95.
44Zadanie 2.96.
44Zadanie 2.97.
45Zadanie 2.98.
45Zadanie 2.99.
45Zadanie 2.100.
45Zadanie 2.101.
45Zadanie 2.102.
46Zadanie 2.103.
46Zadanie 2.104.
46Zadanie 2.105.
46Zadanie 2.106.
47Zadanie 2.107.
47Zadanie 2.108.
47Zadanie 2.112.
48Zadanie 2.113.
48Zadanie 11.
49Zadanie 13.
49Zadanie 14.
50Zadanie 15.
50Zadanie 16.
50Zadanie 17.
50Zadanie 18.
50Zadanie 26.
51Zadanie 27.
51Zadanie 35.
52Zadanie 36.
52Zadanie 37.
52
