Wiedząc, że a, b ∈ (0, 1) i
![]() , udowodnij, że
, udowodnij, że
![]() .
.
T:
![]()
Z: a, b ∈ (0, 1),
![]()
D:
Z równania
![]() wyznacz ln a, wykorzystaj równość
wyznacz ln a, wykorzystaj równość
![]() :
:
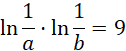
![]()
![]()
![]()
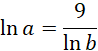
Przekształcaj nierówność do momentu uzyskania nierówności, która jest zawsze prawdziwa. Na początku zlogarytmuj nierówność, możesz to zrobić, ponieważ a, b ∈ (0, 1), czyli ich iloczyn jest większy od 0:
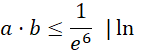
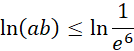
Wykorzystaj równość
![]() oraz równość
oraz równość
![]() :
:
![]()
![]()
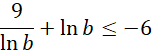
Pomnóż nierówność przez ln b. Pamiętaj o odwróceniu znaku nierówności, ponieważ b ∈ (0, 1), a to oznacza, że ln b jest liczbą mniejszą od 0:
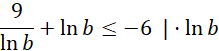
![]()
![]()
Zauważ, że po lewej stronie nierówności występuje wzór skróconego mnożenia
![]() :
:
![]()
Zauważ, że jakakolwiek liczba podniesiona do kwadratu będzie większa od 0 i tylko w przypadku, gdy
![]() będzie równe 0 to nierówność osiągnie 0.
będzie równe 0 to nierówność osiągnie 0.
Podsumowując powyższa nierówność jest zawsze prawdziwa.
Co kończy dowód.

Na początku wyznacz z równania
![]() ln a. Wykorzystaj do tego równość
ln a. Wykorzystaj do tego równość
![]() . Następnie zlogarytmuj nierówność, możesz to wykonać, ponieważ iloczyn a i b jest większy od zera, tak samo jak
. Następnie zlogarytmuj nierówność, możesz to wykonać, ponieważ iloczyn a i b jest większy od zera, tak samo jak
![]() . Następnie przekształć nierówność wykorzystując równości
. Następnie przekształć nierówność wykorzystując równości
![]() oraz
oraz
![]() . Podstaw pod ln a wyznaczoną wartość, a następnie pomnóż przez ln b. Możesz wykonać takie mnożenie, ponieważ b ∈ (0, 1), co oznacza, że podany logarytm będzie przyjmować wartości ujemne, ale nie będzie nigdy 0 ani liczbą dodatnią. Dodatkowo musisz odwrócić znak nierówności, ponieważ mnożysz przez liczbę ujemną. Przenieś wszystko na jedną stronę nierówności i zauważ, że powstał wzór skróconego mnożenia
. Podstaw pod ln a wyznaczoną wartość, a następnie pomnóż przez ln b. Możesz wykonać takie mnożenie, ponieważ b ∈ (0, 1), co oznacza, że podany logarytm będzie przyjmować wartości ujemne, ale nie będzie nigdy 0 ani liczbą dodatnią. Dodatkowo musisz odwrócić znak nierówności, ponieważ mnożysz przez liczbę ujemną. Przenieś wszystko na jedną stronę nierówności i zauważ, że powstał wzór skróconego mnożenia
![]() . Zwróć uwagę na to, że jakakolwiek liczba do kwadratu może dać tylko liczbę większą bądź równą 0. Nic, co zostanie podniesione do kwadratu, nie zwróci liczby ujemnej, a więc nierówność, którą należało udowodnić jest zawsze prawdziwa.
. Zwróć uwagę na to, że jakakolwiek liczba do kwadratu może dać tylko liczbę większą bądź równą 0. Nic, co zostanie podniesione do kwadratu, nie zwróci liczby ujemnej, a więc nierówność, którą należało udowodnić jest zawsze prawdziwa.

Zadanie 2.1.
29Zadanie 2.2.
29Zadanie 2.3.
29Zadanie 2.4.
29Zadanie 2.5.
29Zadanie 2.6.
30Zadanie 2.7.
30Zadanie 2.8.
30Zadanie 2.9.
30Zadanie 2.10.
30Zadanie 2.11.
31Zadanie 2.19.
31Zadanie 2.25.
32Zadanie 2.26.
32Zadanie 2.28.
33Zadanie 2.29.
33Zadanie 2.30.
33Zadanie 2.31.
33Zadanie 2.32.
33Zadanie 2.33.
33Zadanie 2.34.
34Zadanie 2.35.
34Zadanie 2.36.
34Zadanie 2.37.
34Zadanie 2.38.
34Zadanie 2.40.
34Zadanie 2.41.
35Zadanie 2.42.
35Zadanie 2.43.
35Zadanie 2.44.
35Zadanie 2.45.
35Zadanie 2.46.
36Zadanie 2.47.
36Zadanie 2.48.
36Zadanie 2.49.
36Zadanie 2.52.
36Zadanie 2.53.
37Zadanie 2.54.
37Zadanie 2.55.
37Zadanie 2.56.
37Zadanie 2.57.
37Zadanie 2.58.
37Zadanie 2.59.
38Zadanie 2.60.
38Zadanie 2.61.
38Zadanie 2.62.
38Zadanie 2.63.
38Zadanie 2.64.
38Zadanie 2.65.
39Zadanie 2.66.
39Zadanie 2.67.
39Zadanie 2.68.
39Zadanie 2.69.
39Zadanie 2.70.
39Zadanie 2.71.
40Zadanie 2.72.
40Zadanie 2.73.
40Zadanie 2.74.
40Zadanie 2.75.
40Zadanie 2.76.
40Zadanie 2.77.
41Zadanie 2.78.
41Zadanie 2.79.
41Zadanie 2.80.
41Zadanie 2.81.
41Zadanie 2.82.
42Zadanie 2.83.
42Zadanie 2.84.
42Zadanie 2.85.
42Zadanie 2.86.
42Zadanie 2.87.
43Zadanie 2.90.
43Zadanie 2.91.
43Zadanie 2.92.
44Zadanie 2.93.
44Zadanie 2.94.
44Zadanie 2.95.
44Zadanie 2.96.
44Zadanie 2.97.
45Zadanie 2.98.
45Zadanie 2.99.
45Zadanie 2.100.
45Zadanie 2.101.
45Zadanie 2.102.
46Zadanie 2.103.
46Zadanie 2.104.
46Zadanie 2.105.
46Zadanie 2.106.
47Zadanie 2.107.
47Zadanie 2.108.
47Zadanie 2.112.
48Zadanie 2.113.
48Zadanie 11.
49Zadanie 13.
49Zadanie 14.
50Zadanie 15.
50Zadanie 16.
50Zadanie 17.
50Zadanie 18.
50Zadanie 26.
51Zadanie 27.
51Zadanie 35.
52Zadanie 36.
52Zadanie 37.
52
