Dana jest funkcja:
![]()
Udowodnij, że na przedziale (0, 1) jest ona malejąca. Wykorzystaj definicję funkcji malejącej.
Niech x1, x2 będą argumentami funkcji g należącymi do przedziału (0, 1) i takimi, że x1 < x2.
Według definicji funkcji malejącej powyższe argumenty x1 i x2 muszą spełnić zależność:
![]()
![]()
![]()
![]()
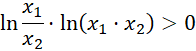
![]()
![]()
Z założeń x1 < x2, zatem ułamek
![]() .
.
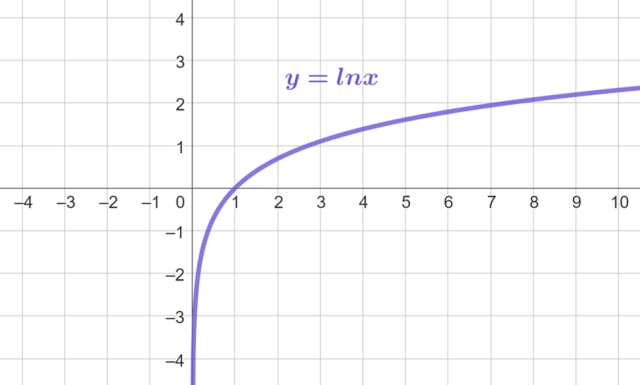
Z wykresu funkcji
![]() można odczytać, że dla x∈ (0, 1) przyjmuje ona wartości ujemne, zatem:
można odczytać, że dla x∈ (0, 1) przyjmuje ona wartości ujemne, zatem:
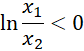
Z założeń x1, x2∈ (0, 1), zatem iloczyn
![]() .
.
Z wykresu funkcji
![]() można odczytać, że dla x∈ (0, 1) przyjmuje ona wartości ujemne, zatem:
można odczytać, że dla x∈ (0, 1) przyjmuje ona wartości ujemne, zatem:
![]()
Wracając do nierówności:
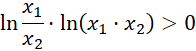
Iloczyn dwóch wyrażeń ujemnych jest dodatni. Nierówność jest zatem prawdziwa, co należało wykazać.

Według definicji funkcji malejącej na danym przedziale, dla dowolnych argumentów x1 i x2 należących do tego przedziału i takich, że x1 < x2, musi być spełniona zależność:
![]() .
.
Zadanie sprowadza się do wykazania powyższej nierówności. Aby to zrobić, Uporządkuj wyrażenie, korzystając z własności:
![]()
![]()
![]()
Doprowadź nierówność do iloczynu w postaci
![]() i oszacuj znak lewej strony wyrażenia. W tym celu posłuż się wykresem funkcji logarytmicznej.
i oszacuj znak lewej strony wyrażenia. W tym celu posłuż się wykresem funkcji logarytmicznej.
W zadaniu pojawia się logarytm naturalny. Jest to logarytm, którego podstawą jest e – liczba Eulera. Jest to wartość stała, a jej przybliżenie wynosi 2,72.

Zadanie 2.1.
29Zadanie 2.2.
29Zadanie 2.3.
29Zadanie 2.4.
29Zadanie 2.5.
29Zadanie 2.6.
30Zadanie 2.7.
30Zadanie 2.8.
30Zadanie 2.9.
30Zadanie 2.10.
30Zadanie 2.11.
31Zadanie 2.19.
31Zadanie 2.25.
32Zadanie 2.26.
32Zadanie 2.28.
33Zadanie 2.29.
33Zadanie 2.30.
33Zadanie 2.31.
33Zadanie 2.32.
33Zadanie 2.33.
33Zadanie 2.34.
34Zadanie 2.35.
34Zadanie 2.36.
34Zadanie 2.37.
34Zadanie 2.38.
34Zadanie 2.40.
34Zadanie 2.41.
35Zadanie 2.42.
35Zadanie 2.43.
35Zadanie 2.44.
35Zadanie 2.45.
35Zadanie 2.46.
36Zadanie 2.47.
36Zadanie 2.48.
36Zadanie 2.49.
36Zadanie 2.52.
36Zadanie 2.53.
37Zadanie 2.54.
37Zadanie 2.55.
37Zadanie 2.56.
37Zadanie 2.57.
37Zadanie 2.58.
37Zadanie 2.59.
38Zadanie 2.60.
38Zadanie 2.61.
38Zadanie 2.62.
38Zadanie 2.63.
38Zadanie 2.64.
38Zadanie 2.65.
39Zadanie 2.66.
39Zadanie 2.67.
39Zadanie 2.68.
39Zadanie 2.69.
39Zadanie 2.70.
39Zadanie 2.71.
40Zadanie 2.72.
40Zadanie 2.73.
40Zadanie 2.74.
40Zadanie 2.75.
40Zadanie 2.76.
40Zadanie 2.77.
41Zadanie 2.78.
41Zadanie 2.79.
41Zadanie 2.80.
41Zadanie 2.81.
41Zadanie 2.82.
42Zadanie 2.83.
42Zadanie 2.84.
42Zadanie 2.85.
42Zadanie 2.86.
42Zadanie 2.87.
43Zadanie 2.90.
43Zadanie 2.91.
43Zadanie 2.92.
44Zadanie 2.93.
44Zadanie 2.94.
44Zadanie 2.95.
44Zadanie 2.96.
44Zadanie 2.97.
45Zadanie 2.98.
45Zadanie 2.99.
45Zadanie 2.100.
45Zadanie 2.101.
45Zadanie 2.102.
46Zadanie 2.103.
46Zadanie 2.104.
46Zadanie 2.105.
46Zadanie 2.106.
47Zadanie 2.107.
47Zadanie 2.108.
47Zadanie 2.112.
48Zadanie 2.113.
48Zadanie 11.
49Zadanie 13.
49Zadanie 14.
50Zadanie 15.
50Zadanie 16.
50Zadanie 17.
50Zadanie 18.
50Zadanie 26.
51Zadanie 27.
51Zadanie 35.
52Zadanie 36.
52Zadanie 37.
52
