Miara kąta wewnętrznego ośmiokąta (n = 8):
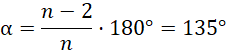
ΔABC – trójkąt równoramienny (boki AB i BC to boki wielokąta foremnego). Zatem kąty przy podstawie AC mają równe miary.
|∡A| = |∡C| = 22,5°
|∡B| = 135°
Miary kątów w ΔABC: 22,5°; 135°; 22,5°
ΔACD
|∡A| = 22,5°
|∡C| = 135° – 22,5° = 112,5°
|∡D| = 180° – (22,5° + 112,5°) = 180° – 135° = 45°
Miary kątów w ΔABC: 22,5°; 112,5°; 45°
ΔADE
|∡A| = 22,5°
|∡D| = 135° – 45° = 90°
|∡E| = 180° – (22,5° + 90°) = 180° – 112,5° = 67,5°
Miary kątów w ΔABC: 22,5°; 90°; 67,5°
ΔAEF
|∡A| = 22,5°
|∡E| = 135° – 67,5° = 67,5°
|∡F| = 180° – (22,5° + 67,5°) = 180° – 90° = 90°
Miary kątów w ΔABC: 22,5°; 67,5°; 90°
ΔAFG
|∡A| = 22,5°
|∡C| = 135° – 90° = 45°
|∡D| = 180° – (22,5° + 45°) = 180° – 67,5° = 112,5°
Miary kątów w ΔABC: 22,5°; 45°; 112,5°
ΔAGH – trójkąt równoramienny (boki AH i HG to boki wielokąta foremnego). Zatem kąty przy podstawie AG mają równe miary.
|∡A| = |∡G| = 22,5°
|∡H| = 135°
Miary kątów w ΔABC: 22,5°; 22,5°; 135°

Przyjrzyj się uważnie rysunkowi. Zauważ, że najdłuższa przekątna dzieli go na dwie przystające figury, w których kąty przy poszczególnych wierzchołkach będą takie same. Znajdź jak najwięcej figur przystających. Pamiętaj, że przekątne poprowadzone z jednego wierzchołka w figurze foremnej dzielą kąt przy tym wierzchołku na równe części. Oblicz miarę kątów wewnętrznych ośmiokąta przy pomocy wzoru: ![]()