W tym zadaniu musisz obliczyć kąt pomiędzy przekątnymi EA i EB w dziewięciokącie.
Od każdego wierzchołka prowadzimy promień do środka okręgu. Powstają w ten sposób kąty równoramienne o kącie między ramionami o mierze ![]()
![]()
![]()
O – środek okręgu opisanego na dziewięciokącie
W trapezie równoramiennym BCDE ∢𝐸𝐷𝐶![]()
![]()
W trójkącie równoramiennym AEO ∢𝐴𝑂𝐸![]()
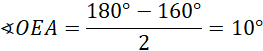
![]()

Dziewięciokąt podziel za pomocą promieni prowadzonych do środka okręgu na dziewięć trójkątów równoramiennych. Zauważ, że kąt między ramionami stanowi jedną dziewiątą koła i oblicz jego miarę. Oblicz miary kątów przy podstawie trójkąta i kąta wewnętrznego dziewięciokąta. Aby uzyskać miarę szukanego kąta, użyj kąta przy wierzchołku E w trapezie równoramiennym ABCD i kąta przy wierzchołku E w trójkącie równoramiennym AOE. Miarę szukanego kąta możesz obliczyć, używając miar kątów przy wierzchołku E, które już znasz.

Ćwiczenie 2
139Zadanie 2
140Zadanie 4
140Ćwiczenie sprawdzające I
141Ćwiczenie 1
146Zadanie 1
147Zadanie 2
147Zadanie 8
148Zadanie 9
148Zadanie dla dociekliwych 3
149Ćwiczenie sprawdzające I
149Ćwiczenie sprawdzające II
149Ćwiczenie sprawdzające III
149Zadanie 8
156Pytanie 1
158Ćwiczenie 1
159Ćwiczenie 2
161Zadanie 1
163Zadanie 4
163Zadanie 5
163Zadanie 10
163Zadanie 12
164Ćwiczenie sprawdzające IV
164Zadanie 1.1
165Zadanie 1.3
165Zadanie 1.4
165Zadanie 1.10
165Zadanie 7
170Zadanie 10
171Zadanie 14
171
