W tym zadaniu musisz obliczyć pole i długość boku dwunastokąta foremnego.
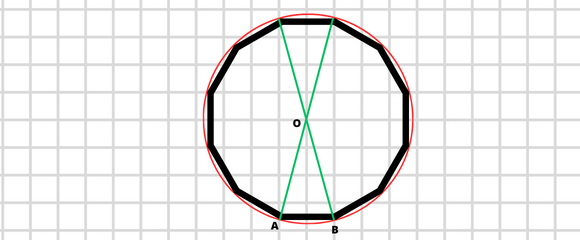
Kąty w trójkącie ABO to ![]()
Poprowadzenie wysokości tego trójkąta z wierzchołka A tworzy trójkąt 30°, 60°, 90°, w którym bok między kątami 60° i 90° to połowa długości boku AO, a więc: ![]()
Pole trójkąta AOB: ![]()
Pole dwunastokąta: ![]()
Jeżeli wysokość AD dzieli bok OB na odcinki OD i DB, to ich długości wynoszą odpowiednie ![]()
Z twierdzenia Pitagorasa bok dwunastokąta wynosi zatem: 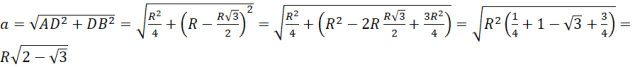

Na początek narysuj dwunastokąt foremny i zaznacz w nim punkty i trójkąty wymienione w poleceniu. Zauważ, że powstaje trójkąt, będący połową trójkąta równobocznego. Skorzystaj z własności i relacji między jego bokami. Następnie oblicz bok dwunastokąta foremnego korzystając z twierdzenia Pitagorasa: ![]()

Ćwiczenie 2
139Zadanie 2
140Zadanie 4
140Ćwiczenie sprawdzające I
141Ćwiczenie 1
146Zadanie 1
147Zadanie 2
147Zadanie 8
148Zadanie 9
148Zadanie dla dociekliwych 3
149Ćwiczenie sprawdzające I
149Ćwiczenie sprawdzające II
149Ćwiczenie sprawdzające III
149Zadanie 8
156Pytanie 1
158Ćwiczenie 1
159Ćwiczenie 2
161Zadanie 1
163Zadanie 4
163Zadanie 5
163Zadanie 10
163Zadanie 12
164Ćwiczenie sprawdzające IV
164Zadanie 1.1
165Zadanie 1.3
165Zadanie 1.4
165Zadanie 1.10
165Zadanie 7
170Zadanie 10
171Zadanie 14
171
